轨迹相似性计算

记得刚接触轨迹相似性计算时，我想着先去找现成的博客快速了解。但找了一圈下来，能搜到的中文资料只有一篇简书的文章，写得还比较笼统，看完也没懂每种方法到底干了什么。然后想起我师兄是做轨迹相似性计算的，于是去翻看他的开题报告，却发现其中关于轨迹相似性方法的介绍居然还是借鉴简书的那篇文章……后来找到了python包可以直接计算，不需要自己去读原文实现各个方法，于是很长一段时间我就止步于“能用就行”。直到我在实验过程中遇到了解释不通的实验结果时，才不得不找来原文读，对这些方法才有了一个清晰的认识。

动笔写此文前又去网上搜了下相关资料，零零散散比三年前多了几篇中文介绍，不过基本上都是对这两年发表的英文综述的翻译和摘抄，于是写下此文，一是介绍这些方法，二是指出一些隐藏的坑，三是附上自己的一点思考，希望能对需要快速入门的人有所帮助。

轨迹相似性计算概述

按照是否考虑时间信息可以将轨迹相似性计算方法分为两类：

1.忽略时间维度，找到具有相似几何形状的轨迹；

2.考虑时间维度，找到在时间上和空间上都相似的轨迹；

这两类方法有不同的应用场景，本文主要介绍第一类方法，即忽略轨迹时间因素的影响，仅考虑轨迹在物理空间中的邻近程度。这类方法也是最常见的。 本节先对这些方法做一个概述，在下一节中会详细介绍各个方法的原理。

传统的轨迹相似性度量方法大多是基于点对匹配来计算轨迹间的距离。欧氏距离（Euclidean distance，ED）也常被称为$L_2$范数，它是一种无参数且具有线性复杂度的距离度量方式，最初是在上世纪60年代针对时序数据所提出的。由于轨迹数据和时序数据具有相似的结构，因此ED后来被用于度量轨迹间的相似性。

但是ED难以处理不同长度轨迹的相似性计算问题。为了解决这一问题，Yi等提出了DTW（Dynamic Time Warping）算法¹，该算法通过递归搜索来找到所有可能的点对组合的最小距离。PDTW²（Piecewise Dynamic Time Warping）是另一种基于动态时间规整的轨迹相似性度量，它是对DTW的改进。

ERP³（Edit distance with Real Penalty）是一种基于编辑距离的轨迹度量方法，该方法引入了一个间隔$g$作为编辑距离的阈值，并使用$L_1$范数作为距离度量来寻求将一条轨迹更改为另一条轨迹所需的最小编辑操作数。

LCSS⁴（Longest common subsequence）是一种著名的距离度量方法，其基本思想是在不更改序列中元素次序的基础上，通过允许两个序列延长来匹配两个序列，同时还允许某些序列元素不匹配。LCSS引入了一个阈值$\epsilon$来确定两个点是否应该匹配，这使得LCSS对噪声和离群值更加稳健。

EDR⁵（Edit Distance on Real sequence）的作者认为ED、DTW和ERP都对轨迹噪声太敏感，LCSS则在区分具有相似公共子序列但不同间隔大小的轨迹时过于粗糙。为了解决上述问题，EDR不仅使用了阈值来缓解噪声的问题，还根据不同的间隔长度对子轨迹间的差异进行相应的惩罚。

EDwP⁶（Edit Distance with Projections）通过线性插值来解决轨迹相似性计算问题中的不一致采样率问题，其优势是不需要设置阈值。这大大减少了轨迹相似性计算的难度，因为一般来说很难确定合适的阈值。

此外，一些数学中的距离度量也被用于轨迹相似性计算中，例如Fréchet距离⁷和Hausdorff距离⁸。

图1是我从自己的毕业论文里截的，给定两条长度分别为$m$和$n$的轨迹$A$、$B$，给出了部分传统轨迹相似性度量方法的细节及其稳健性特点。其中表中的定义给出了方法的具体实现细节，不一致采样率、噪声两个属性分别表示该方法是否具有应对不一致采样率和噪声的能力，无阈值表示该方法是否无需设置距离匹配阈值$\epsilon$​。

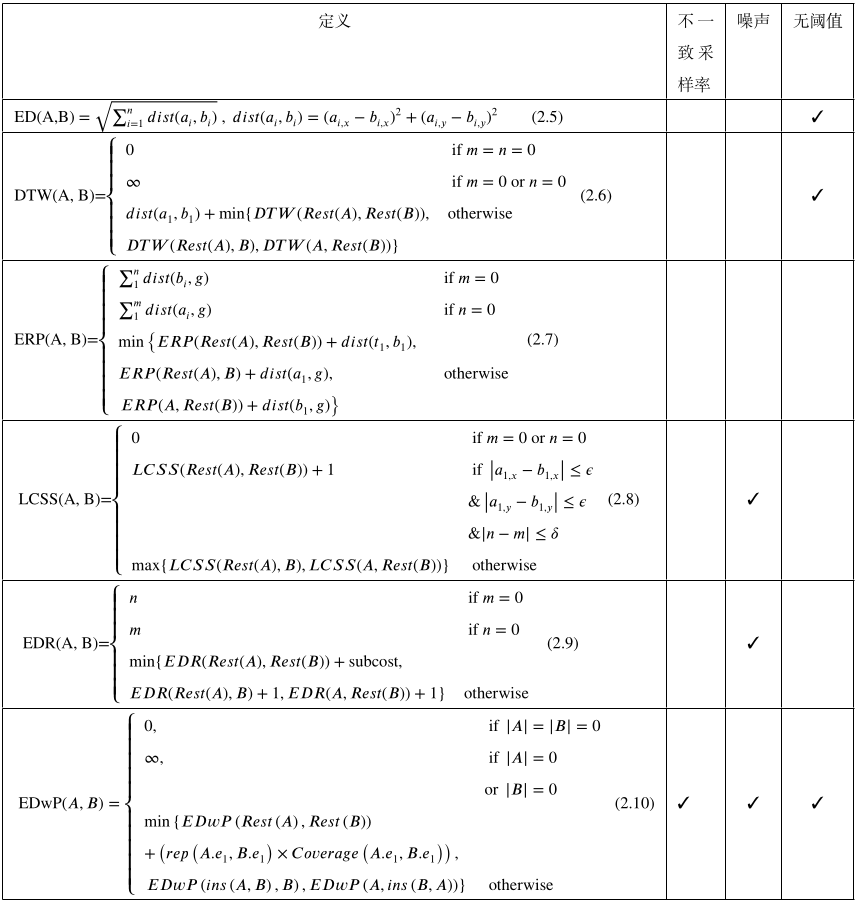
图1. 部分传统轨迹距离度量方法

近年来，也出现了基于深度学习的轨迹相似性计算模型，例如Li等提出了一种基于RNN的模型t2vec⁹，通过学习轨迹的向量表示，并基于轨迹的表示向量来计算轨迹相似性，在部分场景下取得了优于传统方法的结果。针对轨迹数据的不一致采样率和噪声问题，Cao等¹⁰提出了基于单幅图像超分辨率重建技术的轨迹相似性计算方法TrjSR，将低质量轨迹数据表示成低分辨率轨迹图像后，通过超分辨率重建技术得到高分辨率轨迹图像，进而计算轨迹相似性，取得了优于EDwP和t2vec的结果。

详细介绍

接下来详细介绍几种典型的方法。

LCSS

大多数相似性度量方法在数据干净的条件下都能较好地工作。然而受GPS设备的精度限制、较差的信号条件等因素的影响，现实中收集到的轨迹数据通常都不够干净，即存在噪声。LCSS的提出就是为了应对轨迹数据噪声对轨迹相似性计算的影响。LCSS是编辑距离的变种，其基本思想是在允许序列延展、允许部分序列元素不被匹配的前提下匹配两条序列。相比于ED和DTW需要所有序列元素都被匹配（即使有些元素是异常点），LCSS的优势在于允许部分元素不被匹配，因此能在一定程度上克服轨迹数据中异常点对相似性度量的影响。

对于两条轨迹$A=\left(\left(a_{x, 1}, a_{y, 1}\right), \ldots,\left(a_{x, n}, a_{y, n}\right)\right)$​​，$B=\left(\left(b_{x, 1}, b_{y, 1}\right), \ldots,\left(b_{x, m}, b_{y, m}\right)\right)$​​，给定一个整数$\delta$​​和一个实数$0<\epsilon<1$​​，轨迹$A$​​和$B$​​的最长公共子序列长度$LCSS_{\delta, \epsilon}(A, B)$​​的定义如方程$(1.1)$​​所示。其中，$\delta$​​被用来控制两个匹配点在时间上的最大间隔，$\epsilon$​​​是匹配距离的阈值。

显然，最长公共子序列越长，两条轨迹越相似。基于$LCSS_{\delta, \epsilon}(A, B)$可以进一步定义轨迹$A$和$B$​之间的距离：

距离越小越相似。

EDR

EDR的提出同样是针对轨迹数据中的噪声和异常点问题。EDR基于编辑距离来度量两个序列间的相似程度。具体来说，给定两个序列$A$、$B$，$A$和$B$之间的编辑距离是指将$A$中的数据点通过插入、删除和替换操作变换成$B$所需要的操作次数。给定距离阈值$\epsilon$，对于$A$和$B$中的一对采样点$a_i$、$b_j$，如果满足\(\vert a_{1, x}-b_{1, x}\vert \leq \epsilon\)且\(\vert a_{1, y}-b_{1, y}\vert \leq \epsilon\)，则认为$a_i$和$b_j$匹配，相应的编辑距离$subcost=0$；否则$subcost=1$。$EDR(A,B)$的定义如方程$(2.1)$所示。

和LCSS类似，EDR同样引入了距离阈值$\epsilon$来降低噪声对距离度量的影响，因此其在应对异常点的表现上要优于ED、DTW以及ERP。相比于LCSS，EDR会对未匹配的点对施加惩罚，从而获得更准确的度量结果。为了说明这一点，给定下列一维轨迹：$Q=[(t_1,1),(t_2,2),(t_3,3),(t_4,4)]$，$ A=[(t_1,1),(t_2,7),(t_3,2),(t_4,3),(t_5,4)]$，$B=[(t_1,1),(t_2,7),(t_3,8),(t_4,2),(t_5,3),(t_6,4)]$，其中$Q$作为被比较的对象。假设$\epsilon=1$，如果使用LCSS来度量相似性，则$A$和$B$到$Q$的距离相同。然而从数据中可以看出，相比于$B$，显然$A$和$Q$更加相似；如果使用EDR，则$EDR(A,Q)=1$，$EDR(B,Q)=2$，从而可以顺利得出$A$与$Q$​更相似的结果。因此，EDR相比于LCSS对噪声和异常数据更加稳健。

EDwP

尽管LCSS和EDR可以在一定程度上应对噪声的影响，但它们都基于轨迹采样率一致的假设，因此它们都不能很好地处理轨迹数据的不一致采样率问题。此外，它们共同的缺点就是严重依赖距离阈值$\epsilon$，然而$\epsilon$的选取并不容易。$\epsilon$取值不当将会造成不准确的相似性计算结果。例如，沿用上一段中的$Q$、$A$和$B$的例子，如果$\epsilon=5$，则EDR和LCSS都会判定$A$到$Q$和$B$到$Q$的距离为0，从而造成了不准确的度量结果。

EDwP是一种不需要参数的轨迹相似性度量方法，它基于编辑距离，使用动态插值的方法来解决轨迹数据的不一致采样率问题。EDwP使用了两种编辑操作，即替换（replacement）和插入（insert）来匹配两条轨迹间的采样点。

替换操作用$rep\left(e_{1},e_{2}\right)$来表示，其中$e_1$和$e_2$​是待匹配的轨迹段。替换操作的代价定义为：

其中，$s_1$和$s_2$分别表示轨迹段$e$的首端点和尾端点，$dist\left(s_1,s_2\right)$表示$s_1$和$s_2$之间的欧氏距离。

插入操作$ins\left(e_{1},e_{2}\right)$是指通过向$e_1$中插入一个点$p^{ins\left(e_{1},e_{2}.s_2\right)}$，将$e_1$划分成两段$\left[e_1.s_1,p^{ins\left(e_{1},e_{2}.s_2\right)}\right]$和$\left[p^{ins\left(e_{1},e_{2}.s_2\right)},e_1.s_2\right]$，使得划分后的第一段$\left[e_1.s_1,p^{ins\left(e_{1},e_{2}.s_2\right)}\right]$和$e_2$可以实现最佳匹配。因此，$p^{ins\left(e_{1},e_{2}.s_2\right)}$是$e_1$上与$e_2.s_2$​距离最近的点：

$ins\left(e_{1},e_{2}\right)$操作并不会产生任何代价，$e_1$​被划分后的第一段会在下一步计算中产生代价。

根据上述编辑操作，轨迹$A$、$B$间的EDwP距离被定义为方程$(3.3)$。其中$Coverage\left(e_1,e_2\right)=length(e_1)+length(e_2)$​​，它表示长度越长的轨迹段在计算编辑距离代价时拥有更大的权重。

t2vec

有别于上述基于点对匹配的轨迹相似性计算方法，t2vec是一种基于深度表征学习的轨迹相似性计算方法，通过学习轨迹的表示向量来缓解轨迹数据中不一致采样率和噪声的影响。具体来说，t2vec采用了基于RNN的Seq2Seq结构，其中主要包括编码器（encoder）和解码器（decoder）两部分，如图2所示，其中模型输入为序列$x$，输出为序列$y$，EOS是序列的终止标识符，$v$是$x$的表示向量。隐藏状态$h_t$压缩了$\left[x,y_1,y_2,\cdots,y_{t-1}\right]$中的序列信息。编码器负责将序列$x$中的信息编码成为一个固定维度的向量$v$，解码器则负责从编码表示$v$中解码出序列$y$​。由于RNN要求输入为实值向量，因此需要使用符号嵌入层（token embedding layer）将离散的符号嵌入成向量。

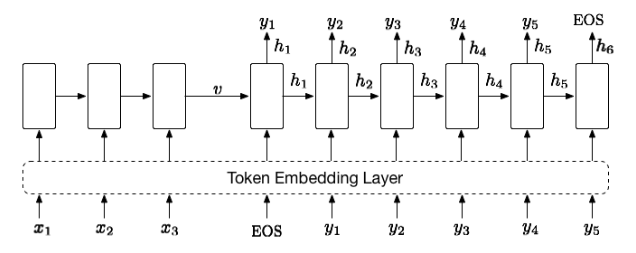
图2. Seq2Seq 模型

t2vec通过有监督学习的方式来学习从低采样率轨迹到高采样率轨迹的映射，这种方式可以让模型从训练数据中学习到如何对低采样率轨迹中缺失的和不准确的轨迹点进行填补，从而能尽可能地从轨迹信息中恢复出潜在的路径信息。t2vec使用编码后的向量$v$作为轨迹的向量表示，在GPU的加持下可以在$O(n)$的时间复杂度内将长度为$n$的轨迹表示成向量，进而可以基于轨迹表示向量间的欧氏距离来度量轨迹间的相似性，时间复杂度为\(O(\vert v \vert)\)。因此该方法度量轨迹相似性的时间复杂度为\(O(n+\vert v \vert)\)，相比于传统方法的$O(n^2)$时间复杂度是一个很大的提升。

TrjSR

上述的所有方法都是在基于轨迹的序列形式做文章，但使用轨迹序列存在以下三个问题：

1. 轨迹序列不能显式地反映轨迹数据的空间特征：空间上邻近的轨迹点不一点在序列中邻近；
2. 使用RNN在测试阶段会遇到误差累积¹¹的问题：RNN基于之前预测出的结果来预测下一个轨迹点，误差会在预测过程中累积；
3. 基于序列的轨迹相似性计算方法不便于比较形状相似但次序相反的轨迹：例如，一个人的通勤轨迹包括从家到公司和从公司回家，这两条轨迹采样自同一路径，因此在空间上相似，但基于序列的方法不便于处理这种情况。

针对上述问题，TrjSR通过将轨迹数据表示成为灰度轨迹图像予以解决。采样率不一致和存在噪声的轨迹数据被表示成为低质量轨迹图像，通过超分辨率成像技术重建出超分辨率轨迹图像后，再被嵌入成低维轨迹向量去计算相似性。相比于低分辨率轨迹图像，生成的超分图像拥有更多的细节，填补了轨迹数据中缺失的和不准确的部分，提升了轨迹质量，从而得到了更准确的相似性计算结果。

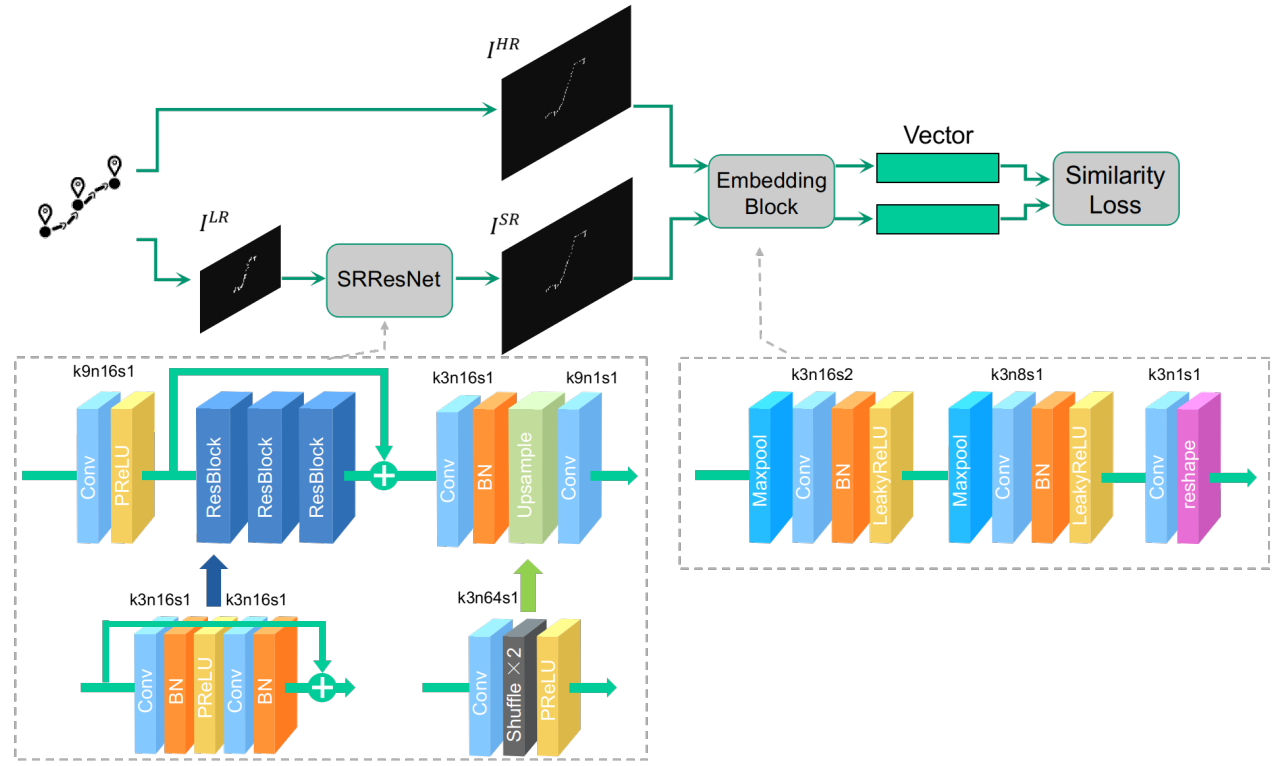
Fréchet距离

Fréchet距离以Maurice Fréchet的名字命名，它是数学中度量曲线间相似度的一种方法，其考虑了曲线中点的位置和顺序。两条曲线之间的Fréchet距离是指在从头到尾遍历两条曲线的过程中，连接两条曲线所需线段的最小长度。

假定$S$是一个度量空间，$d$是$S$上的度量函数。$S$中的曲线是从单位区间到$S$的连续映射，例如$A:[0,1]\rightarrow S$。$[0,1]$上的重参数化函数$\alpha$是指一个连续、非递减的满射$\alpha:[0,1]\rightarrow[0,1]$。给定$S$中的两条曲线$A$、$B$和$[0,1]$上的重参数化函数$\alpha$和$\beta$，$A$和$B$的Fréchet距离被定义为$A(\alpha(t))$和$B(\beta(t))$在$[0,1]$​​上最大距离的下确界。其数学定义为：

Hausdorff距离

Hausdorff距离在数学中被用来计算度量空间中两个子集之间的距离。它指的是从一个集合中的点到另一个集合中与其最接近的点的最大距离，如图3所示:

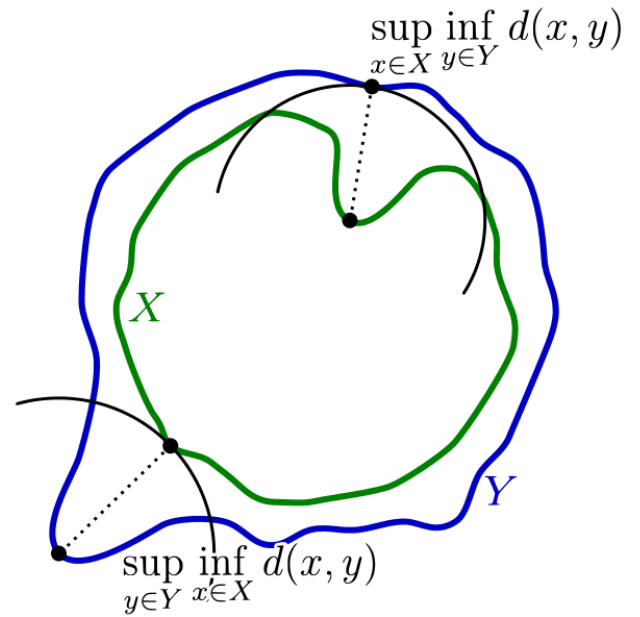
图3. 计算绿线 𝑋 和蓝线 𝑌 间 Hausdorff 距离的组成部分

给定度量空间$S$中的两个子集$X$和$Y$​，Hausdorff距离的形式化定义如下：

其中$d$​​是度量函数。

一些坑

traj_dist包

轨迹相似性计算（或者叫轨迹距离度量）在网上能找到的python包基本上就只有一个traj_dist，只有一百多个star，小众程度可见一斑。这一方面是因为这个研究方向没有太多可做的空间，像DTW这种经典的方法在大多数场景下都非常好用，目前学术界的工作大多集中在提升相似性计算的效率上；另一方面是因为这些经典的方法实现起来也不难，而且它们隶属于序列间距离度量这个更一般的问题，我没有去找，但应该也有人针对序列距离计算实现了类似的包。

但不管怎样，traj_dist的作者把这些常用的轨迹距离度量方法打包在一起的确方便了广大使用者，事实上用起来也非常友好。作者是用Cython实现的，比我自己用python实现的要快很多（但用java会更快）。

但是，包中关于EDR的实现有误。这是源码：

def c_e_edr(np.ndarray[np.float64_t,ndim=2] t0, np.ndarray[np.float64_t,ndim=2] t1, float eps):
    """
    Usage
    -----
    The Edit Distance on Real sequence distance between trajectory t0 and t1.
    Parameters
    ----------
    param t0 : len(t0)x2 numpy_array
    param t1 : len(t1)x2 numpy_array
    eps : float
    Returns
    -------
    edr : float
           The Edit Distance on Real sequence distance between trajectory t0 and t1
    """
    cdef int n0,n1,i,j,subcost
    cdef np.ndarray[np.float64_t,ndim=2] C
    cdef double x0,y0,x1,y1,lcss

    n0 = len(t0)+1
    n1 = len(t1)+1

    # An (m+1) times (n+1) matrix
    C=np.zeros((n0,n1)) # 这里有问题

    for i from 1 <= i < n0:
        for j from 1 <= j < n1:
            x0=t0[i-1,0]
            y0=t0[i-1,1]
            x1=t1[j-1,0]
            y1=t1[j-1,1]
            if c_eucl_dist(x0,y0,x1,y1)<eps:
                subcost = 0
            else:
                subcost = 1
            C[i,j] = fmin(fmin(C[i,j-1]+1, C[i-1,j]+1),C[i-1,j-1]+subcost)
    edr = float(C[n0-1,n1-1])/fmax(n0-1,n1-1) # 这里做了类似归一化的处理
    return edr

根据公式$(2.1)$，两条轨迹中一旦有一条轨迹的长度为0，则距离直接取另一条轨迹的长度。但是在traj_dist的实现中，遇到这种情况时距离会取0：

C=np.zeros((n0,n1)) # 这里有问题

而且作者对最终的结果除以最长的轨迹长度，其目的是想缓解长轨迹对存在的编辑距离过大的问题，但这并不是EDR原文中的操作。事实上一旦遇到轨迹对中的两条轨迹长度相差过大，即一条轨迹过长，而另一条轨迹又过短，就会造成EDR距离取值过小的问题。

当然这两处修改起来也不难，直接在源码中修改后再编译一下即可：

# 对第一处问题的修改
C=np.zeros((n0,n1))
for i in range(1,n0):
    C[i][0] = i
    for j in range(1,n1):
        C[0][j] = j
        
# 对第二处问题的修改
edr = float(C[n0-1,n1-1])
   

EDwP的实现

EDwP的作者用java实现了上述这些经典的轨迹距离度量方法，并且开源出来。这套代码的优点是用java实现，所以计算速度更快；缺点是没有文档和必要的注释，给的example也极其简单，需要解压jar文件去读懂他的代码，然后再按自己的需求调用他的函数。

这套代码同样是实现EDR的部分有误，问题依然是出在处理长度为0的轨迹时：

public double[] getDistance(Trajectory t1, Trajectory t2) {
        this.matrix = new Matrix(t1.edges.size() + 2, t2.edges.size() + 2);
        this.initializeMatrix(t1.edges.size() + 1, t2.edges.size() + 1);
        for (int i = 1; i < this.matrix.numRows(); ++i) {
            for (int j = 1; j < this.matrix.numCols(); ++j) {
                boolean subcost = !(t1.getPoint(i - 1).euclidean(t2.getPoint(j - 1)) <= 			this.sThresh);	
                this.matrix.value[i][j] = Math.min(this.matrix.value[i - 1][j - 1] + (double)subcost, Math.min(this.matrix.value[i - 1][j] + 1.0, this.matrix.value[i][j - 1] + 1.0));
            }
        }
        double[] answer = new double[]{this.matrix.score(), -1.0};
        return answer;
    }

private void initializeMatrix(int n, int m) {
    int i;
    for (i = 0; i < this.matrix.numRows(); ++i) {
        Arrays.fill(this.matrix.value[i], 0.0);
    }
    for (i = 1; i < this.matrix.value.length; ++i) {
        this.matrix.value[i][0] = m;
    }
    for (int j = 1; j < this.matrix.value[0].length; ++j) {
        this.matrix.value[0][j] = n;
    }
}

从initializeMatrix函数可以看到，当一条轨迹的长度为0时，作者将EDR距离取为两条轨迹的原始长度m或n，这两个值是不变的。但实际上，由于EDR是动态规划算法，每一个子问题处理的都是子轨迹，而不同子问题中的子轨迹的长度是不同的，因此应该取当前子问题中两条子轨迹的长度用于初始化。

事实上，一旦改正上述错误的实现，EDR的结果会更好，甚至在一些测试条件下的结果比EDwP还要好，而并不是像EDwP原文里写的EDwP在所有测试条件下都取得最优。我给原作者发过邮件，但并没有收到回复，嗯…既意外又不意外。

一些思考

据我浅薄的了解，轨迹相似度计算在2000年之后的研究工作不外乎两类：1）提升低质量数据下的计算准确率；2）提高大规模数据的计算和检索效率。两者的热度大概以深度学习的中期为分水岭。

前者解决的具体问题包括轨迹数据中的噪声、不一致采样率等问题。然而，这些问题虽然确实存在，但并不广泛存在。这就造成了一种尴尬的局面：这些精巧的算法能够在差的数据上取得更准确的结果，但差的数据毕竟是少数。学术文章为了彰显自己的价值故意放大了数据质量问题的严重性，但实际中完全可以通过其他技术手段提高数据的质量，或是直接去除这部分低质量数据。事实上，从我的自己的实验来看，在正常数据上，DTW、EDR这两个经典算法的效果已经非常好了；在质量没那么低的数据上，经典算法的结果也是可以接受的。

后者是在深度学习进入中期后，以及准确计算轨迹相似性已无太多可做空间的背景下壮大起来的。其核心思想是利用神经网络将轨迹数据嵌入成低维向量再去计算相似性。优点是使用低维向量可以快速计算和检索，缺点是无法保证轨迹在嵌入到低维空间后依然精确保持原有的相似关系，所以这类工作几乎都是牺牲部分准确性去换取高效率。