在有了对抗样本之后,如何用其去训练稳健的模型来抵抗攻击?承接上一章内容,本章给出两种方法。
从对抗样本到训练稳健模型
在之前的章节中我们主要关注的是如何求解内部最大化问题,即 \(\DeclareMathOperator*{\maximize}{maximize} \maximize_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\) 我们介绍了三种方法来求解:基于局部梯度(可以给出目标的下界)、组合优化(可以精确求解优化目标)以及凸松弛(可以给出目标的上界)。
在本章节中我们回到第一章中提到的最小-最大问题,即训练一个针对对抗攻击稳健的模型。换句话说,不管是什么样的针对性攻击(尤其是我们不知道攻击者采用了哪种攻击策略),我们希望模型都能表现良好。即,给定一组输入/输出对$S$,我们想要求解如下的外部最小化问题:
\[\DeclareMathOperator*{\minimize}{minimize} \minimize_\theta \frac{1}{|S|} \sum_{x,y \in S} \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]最小-最大的顺序很重要。具体的,最大化是在最小化的内部,这意味着攻击方(试图最大化损失)是后手操作(即在得知了模型信息后再进行攻击)。我们基本上都是假设对手完全了解分类器的参数(这也是之前章节里的潜在假设),所以稳健性优化的目标是即使对手知道模型的全部信息,也能保证模型不被攻击。当然,在实际操作中我们也可以寄希望于对手的“能力”也许求解不了针对大型模型的整数规划,不过很难给出对方“能力”的精确定义,因此在评估模型时应格外小心,以应对可能的“真实”对手。
好消息是,从某种意义上讲当我们在介绍各种方法来近似解决内部最大化问题时,就已经在为对抗训练做了很多工作。对于求解内部最大化问题的三种方法,都有相应的等效方式来训练稳健的系统。然而,第二种方法(即通过组合优化求解精确解)实际上是不可行的 ,这是因为求解整数规划已经非常耗时了,如果还要将其进一步整合到训练过程中就更加无法接受(实际上,我们需要一个变量数目等于隐单元的个数的整数规划,每一个样本上的每一轮训练都要计算一次)。因此我们不考虑将组合优化方法整合到训练过程中。还剩下了两种选择:
- 使用下界,和通过局部搜索方法(也就是梯度下降方法)构造的样本来(经验地)训练一个对抗性稳健的分类器。
- 使用凸上界来训练一个可证明的稳健分类器。
这两种方法之间也有权衡:尽管第一种方法似乎不太理想,但事实证明,第一种方法能凭经验创建强大的模型(根据我们能得到的最好的攻击样本,经验地获得更好的稳健性)。因此,在确定如何最好地去构建对抗稳健模型时,需要认证权衡这两种策略。
使用对抗样本的对抗训练
这一策略非常简单,就是生成对抗样本,然后将其用于训练。换句话说,因为标准的训练过程会使得模型对于容易受到对抗样本的影响,所以我们就用一些对抗样本来训练模型。
那么问题来了:该使用哪些对抗样本呢?假设我们希望使用梯度下降来优化最小-最大目标
\[\DeclareMathOperator*{\minimize}{minimize} \minimize_\theta \frac{1}{|S|} \sum_{x,y \in S} \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]例如使用随机梯度下降,只需要在minibatch上迭代计算损失函数关于$\theta$的梯度,并沿负梯度方向更新,即
\[\theta := \theta - \alpha \frac{1}{|B|} \sum_{x,y \in B} \nabla_\theta \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]至于如何计算内部项的梯度,正如我们在第一章提到的,只需要利用Danskin’s Theorem:1) 找到最大值;2) 计算在该值下的梯度。即,
\[\DeclareMathOperator*{\argmax}{argmax} \nabla_\theta \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y) = \nabla_\theta \ell(h_\theta(x + \delta^\star(x)), y)\]其中,
\[\delta^\star(x) = \argmax_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]然而,Danskin’s theorem成立的前提是我们能够找到最大值。但根据上一章节,我们知道想找到最大值并不容易。尽管如此,在实践中我们发现:稳健的梯度下降过程的“质量”和我们求解最大化问题的程度紧密相关,求解得越好,Danskin’s theorem似乎就越接近成立。换句话说,对抗训练的关键是将“强大”的攻击纳入训练过程中。
具体的策略如下:
\[% <![CDATA[ \begin{split} & \mbox{Repeat:} \\ & \quad \mbox{1. Select minibatch $B$, initialize gradient vector $g := 0$} \\ & \quad \mbox{2. For each $(x,y)$ in $B$:} \\ & \quad \quad \mbox{a. Find an attack perturbation $\delta^\star$ by (approximately) optimizing } \\ & \qquad \qquad \qquad \delta^\star = \argmax_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y) \\ & \quad \quad \mbox{b. Add gradient at $\delta^\star$} \\ & \qquad \qquad \qquad g:= g + \nabla_\theta \ell(h_\theta(x + \delta^\star), y) \\ & \quad \mbox{3. Update parameters $\theta$} \\ & \qquad \qquad \qquad \theta:= \theta - \frac{\alpha}{|B|} g \end{split} %]]>\]尽管上述操作能近似地优化稳健损失,不过在实际中我们通常也会在原始点处做标准的优化(即在不做扰动的情况下求取梯度并更新),因为这样能稍微提升在“标准”误差上的表现(即无攻击情况下)。此外,还经常会为PGD使用随机化技术(即随机选择初始点),否则损失平面会出现问题,以至于仅在与训练样本相同的点处的梯度指向“浅”方向(损失较小);但是在靠近这些点非常近的地方,损失平面会非常陡峭(损失较大)(我的理解是,如果只在某些点上做优化,那么网络在处理稍微不同的点时,会由于未对该点做优化而表现差,换句话说,解空间是不全面的)。
整体代码如下,其中借用了上一章的部分代码来创建和训练模型,以及产生对抗样本。
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
mnist_train = datasets.MNIST("../data", train=True, download=True, transform=transforms.ToTensor())
mnist_test = datasets.MNIST("../data", train=False, download=True, transform=transforms.ToTensor())
train_loader = DataLoader(mnist_train, batch_size = 100, shuffle=True)
test_loader = DataLoader(mnist_test, batch_size = 100, shuffle=False)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
torch.manual_seed(0)
class Flatten(nn.Module):
def forward(self, x):
return x.view(x.shape[0], -1)
model_cnn = nn.Sequential(nn.Conv2d(1, 32, 3, padding=1), nn.ReLU(),
nn.Conv2d(32, 32, 3, padding=1, stride=2), nn.ReLU(),
nn.Conv2d(32, 64, 3, padding=1), nn.ReLU(),
nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU(),
Flatten(),
nn.Linear(7*7*64, 100), nn.ReLU(),
nn.Linear(100, 10)).to(device)
def fgsm(model, X, y, epsilon=0.1):
""" Construct FGSM adversarial examples on the examples X"""
delta = torch.zeros_like(X, requires_grad=True)
loss = nn.CrossEntropyLoss()(model(X + delta), y)
loss.backward()
return epsilon * delta.grad.detach().sign()
def pgd_linf(model, X, y, epsilon=0.1, alpha=0.01, num_iter=20, randomize=False):
""" Construct FGSM adversarial examples on the examples X"""
if randomize:
delta = torch.rand_like(X, requires_grad=True)
delta.data = delta.data * 2 * epsilon - epsilon
else:
delta = torch.zeros_like(X, requires_grad=True)
for t in range(num_iter):
loss = nn.CrossEntropyLoss()(model(X + delta), y)
loss.backward()
delta.data = (delta + alpha*delta.grad.detach().sign()).clamp(-epsilon,epsilon)
delta.grad.zero_()
return delta.detach()
唯一的修改就是加入了对抗训练的部分。
def epoch(loader, model, opt=None):
"""Standard training/evaluation epoch over the dataset"""
total_loss, total_err = 0.,0.
for X,y in loader:
X,y = X.to(device), y.to(device)
yp = model(X)
loss = nn.CrossEntropyLoss()(yp,y)
if opt:
opt.zero_grad()
loss.backward()
opt.step()
total_err += (yp.max(dim=1)[1] != y).sum().item()
total_loss += loss.item() * X.shape[0]
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
def epoch_adversarial(loader, model, attack, opt=None, **kwargs):
"""Adversarial training/evaluation epoch over the dataset"""
total_loss, total_err = 0.,0.
for X,y in loader:
X,y = X.to(device), y.to(device)
delta = attack(model, X, y, **kwargs)
yp = model(X+delta)
loss = nn.CrossEntropyLoss()(yp,y)
if opt:
opt.zero_grad()
loss.backward()
opt.step()
total_err += (yp.max(dim=1)[1] != y).sum().item()
total_loss += loss.item() * X.shape[0]
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
首先训练一个标准模型并评估其对抗误差。
opt = optim.SGD(model_cnn.parameters(), lr=1e-1)
for t in range(10):
train_err, train_loss = epoch(train_loader, model_cnn, opt)
test_err, test_loss = epoch(test_loader, model_cnn)
adv_err, adv_loss = epoch_adversarial(test_loader, model_cnn, pgd_linf)
if t == 4:
for param_group in opt.param_groups:
param_group["lr"] = 1e-2
print(*("{:.6f}".format(i) for i in (train_err, test_err, adv_err)), sep="\t")
torch.save(model_cnn.state_dict(), "model_cnn.pt")
0.272300 0.031000 0.666900
0.026417 0.022000 0.687600
0.017250 0.020300 0.601500
0.012533 0.016100 0.673000
0.009733 0.014400 0.696600
0.003850 0.011000 0.705400
0.002833 0.010800 0.696800
0.002350 0.010600 0.707500
0.002033 0.010900 0.714600
0.001783 0.010600 0.708300
model_cnn.load_state_dict(torch.load("model_cnn.pt"))
正如我们看到的那样,“标准”误差(即clean error)非常低,但对抗误差非常高(并且随着训练过程而上升)。接下来我们做同样的操作,只不过这次我们使用对抗训练。
model_cnn_robust = nn.Sequential(nn.Conv2d(1, 32, 3, padding=1), nn.ReLU(),
nn.Conv2d(32, 32, 3, padding=1, stride=2), nn.ReLU(),
nn.Conv2d(32, 64, 3, padding=1), nn.ReLU(),
nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU(),
Flatten(),
nn.Linear(7*7*64, 100), nn.ReLU(),
nn.Linear(100, 10)).to(device)
opt = optim.SGD(model_cnn_robust.parameters(), lr=1e-1)
for t in range(10):
train_err, train_loss = epoch_adversarial(train_loader, model_cnn_robust, pgd_linf, opt)
test_err, test_loss = epoch(test_loader, model_cnn_robust)
adv_err, adv_loss = epoch_adversarial(test_loader, model_cnn_robust, pgd_linf)
if t == 4:
for param_group in opt.param_groups:
param_group["lr"] = 1e-2
print(*("{:.6f}".format(i) for i in (train_err, test_err, adv_err)), sep="\t")
torch.save(model_cnn_robust.state_dict(), "model_cnn_robust.pt")
0.715433 0.068900 0.170200
0.100933 0.020500 0.062300
0.053983 0.016100 0.046200
0.040100 0.011700 0.036400
0.031683 0.010700 0.034100
0.021767 0.008800 0.029000
0.020300 0.008700 0.027600
0.019050 0.008700 0.027900
0.019150 0.008600 0.028200
0.018250 0.008500 0.028300
model_cnn_robust.load_state_dict(torch.load("model_cnn_robust.pt"))
评估稳健模型
可以看到,相比于标准训练下71%的对抗误差,对抗训练后我们可以将对抗误差降至2.8%(同时标准误差也得到了降低,不过需要强调的是,这种clean error的降低只是在MNIST数据集上如此,并不是通用的结果)。这似乎是巨大的成功!
但请务必小心再小心。每当我们针对某类特定的攻击去对抗训练网络,都会非常容易地在对抗该特定攻击上有出色的表现。从某种程度上说,这正是神经网络的特性:它们会在训练集上做出精准预测。如果我们进行其它的攻击呢?比如FGSM,或者PGD运行的时间再久一点?或者使用上随机化?再或者未来有人用了某种效果更好的优化算法来进行攻击?
为了了解这一点,我们首先尝试FGSM。
print("FGSM: ", epoch_adversarial(test_loader, model_cnn_robust, fgsm)[0])
FGSM: 0.0258
嗯这个倒不错。不过事实上FGSM确实比PGD攻击也差一些(再上一章中有说明),所以这个不奇怪。我们再试试运行PGD更久一些。
print("PGD, 40 iter: ", epoch_adversarial(test_loader, model_cnn_robust, pgd_linf, num_iter=40)[0])
PGD, 40 iter: 0.0286
也不错!虽然误差上升了一点,不过也在合理的范围内(如果你运行得再久一些会发现误差不会改变太多……这是因为这些样本限制了$\ell_\infty$球的边界,运行更多步并不会改变什么)。但是如果我们使用更小的步长多运行一会儿,来试试更“细粒度”(fine-grained)的攻击呢?
print("PGD, small_alpha: ", epoch_adversarial(test_loader, model_cnn_robust, pgd_linf, num_iter=40, alpha=0.05)[0])
PGD, 40 iter: 0.0284
误差还是没什么变化,我们对这个模型越来越有信心了。然后我们再加上随机化。
print("PGD, randomized: ", epoch_adversarial(test_loader, model_cnn_robust, pgd_linf,
num_iter=40, randomize=True)[0])
PGD, randomized: 0.0284
好的,至此我们已经做了足够多的评估,或许我们可以自信地将模型放到线上看看别人是否能攻破它(注意,线上的模型并不是这个,不过确实是以同样的方式训练得到的)。当然我们也还需要尝试其他可能的优化器、尝试多种随机策略等等。
注意:还有一种没那么相关的评估是看模型对于不同扰动攻击的效果,比如针对$\ell_\infty$稳健的模型是否对$\ell_2$攻击也稳健?这个要求确实有点高了,毕竟针对$\ell_\infty$攻击训练的模型,当然不太会在其它类型的攻击下也表现稳健。当然,如果有人确实想要实现那种“泛化”的稳健模型的话,那么确实需要考虑这一点。除此之外,还有那种人类看起来觉得“相同”的攻击样本,这就更难去形式化了,是在未来值得研究的问题。
这些稳健的模型到底发生了什么?
所以为什么稳健模型能够抵挡对抗攻击呢?想回答这一问题,一种办法是将损失平面投影到二维平面上(一维是真实梯度方向,另一维是随机方向)。
for X,y in test_loader:
X,y = X.to(device), y.to(device)
break
def draw_loss(model, X, epsilon):
Xi, Yi = np.meshgrid(np.linspace(-epsilon, epsilon,100), np.linspace(-epsilon,epsilon,100))
def grad_at_delta(delta):
delta.requires_grad_(True)
nn.CrossEntropyLoss()(model(X+delta), y[0:1]).backward()
return delta.grad.detach().sign().view(-1).cpu().numpy()
dir1 = grad_at_delta(torch.zeros_like(X, requires_grad=True))
delta2 = torch.zeros_like(X, requires_grad=True)
delta2.data = torch.tensor(dir1).view_as(X).to(device)
dir2 = grad_at_delta(delta2)
np.random.seed(0)
dir2 = np.sign(np.random.randn(dir1.shape[0]))
all_deltas = torch.tensor((np.array([Xi.flatten(), Yi.flatten()]).T @
np.array([dir2, dir1])).astype(np.float32)).to(device)
yp = model(all_deltas.view(-1,1,28,28) + X)
Zi = nn.CrossEntropyLoss(reduction="none")(yp, y[0:1].repeat(yp.shape[0])).detach().cpu().numpy()
Zi = Zi.reshape(*Xi.shape)
#Zi = (Zi-Zi.min())/(Zi.max() - Zi.min())
fig = plt.figure(figsize=(10,10))
ax = fig.gca(projection='3d')
ls = LightSource(azdeg=0, altdeg=200)
rgb = ls.shade(Zi, plt.cm.coolwarm)
surf = ax.plot_surface(Xi, Yi, Zi, rstride=1, cstride=1, linewidth=0,
antialiased=True, facecolors=rgb)
标准网络的损失平面如下。
draw_loss(model_cnn, X[0:1], 0.1)
损失增长得很快。再来看稳健模型的损失平面。
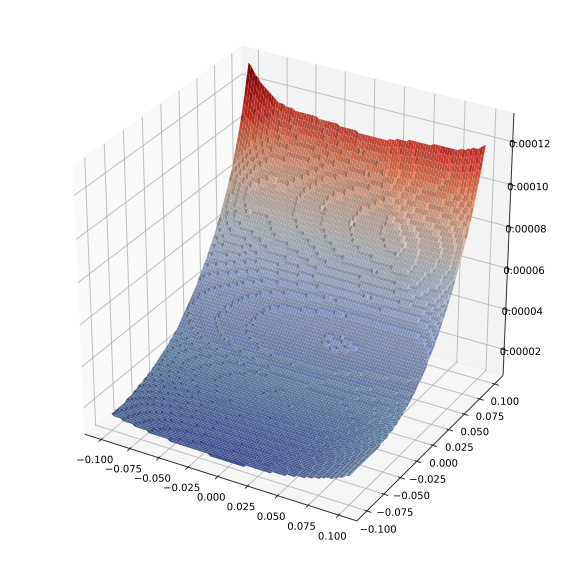
draw_loss(model_cnn_robust, X[0:1], 0.1)
对比两者在$z$轴上的尺度会发现(第二张图中的“凹凸”是缩小了$z$轴范围的结果,若将其换作与第一张图相同的尺度就会变得完全平坦),稳健模型的损失平面在梯度方向上非常平坦(该方向本应该是最陡的方向),而在随机方向上,传统训练的模型在梯度方向和(在梯度方向上移动后)在随机方向上变化都非常快。当然,这当然不能保证不会出现损失急剧上升的情况,但至少暗示了大致的情况。
总的来说,基于PGD的对抗训练的模型确实稳健,其损失平面本身具有光滑的损失平面,而不仅仅是通过某些“技巧”隐藏了损失增加的方向。是否能够真正地断言稳健还有待观察,这也是目前正在研究的一个主题。
基于松弛的稳健训练
作为最后一块拼图,我们尝试用凸松弛不单单去验证稳健性,也用其进行训练。这里我们聚焦于基于区间界(相比于凸松弛线性规划,计算量更小)。
首先,我们考虑使用区间界来验证我们刚刚训练的稳健分类器的稳健性。回想一下,若针对所有类别的优化目标值都是正数,则分类器被验证可以抵抗攻击。
def bound_propagation(model, initial_bound):
l, u = initial_bound
bounds = []
for layer in model:
if isinstance(layer, Flatten):
l_ = Flatten()(l)
u_ = Flatten()(u)
elif isinstance(layer, nn.Linear):
l_ = (layer.weight.clamp(min=0) @ l.t() + layer.weight.clamp(max=0) @ u.t()
+ layer.bias[:,None]).t()
u_ = (layer.weight.clamp(min=0) @ u.t() + layer.weight.clamp(max=0) @ l.t()
+ layer.bias[:,None]).t()
elif isinstance(layer, nn.Conv2d):
l_ = (nn.functional.conv2d(l, layer.weight.clamp(min=0), bias=None,
stride=layer.stride, padding=layer.padding,
dilation=layer.dilation, groups=layer.groups) +
nn.functional.conv2d(u, layer.weight.clamp(max=0), bias=None,
stride=layer.stride, padding=layer.padding,
dilation=layer.dilation, groups=layer.groups) +
layer.bias[None,:,None,None])
u_ = (nn.functional.conv2d(u, layer.weight.clamp(min=0), bias=None,
stride=layer.stride, padding=layer.padding,
dilation=layer.dilation, groups=layer.groups) +
nn.functional.conv2d(l, layer.weight.clamp(max=0), bias=None,
stride=layer.stride, padding=layer.padding,
dilation=layer.dilation, groups=layer.groups) +
layer.bias[None,:,None,None])
elif isinstance(layer, nn.ReLU):
l_ = l.clamp(min=0)
u_ = u.clamp(min=0)
bounds.append((l_, u_))
l,u = l_, u_
return bounds
def interval_based_bound(model, c, bounds, idx):
# requires last layer to be linear
cW = c.t() @ model[-1].weight
cb = c.t() @ model[-1].bias
l,u = bounds[-2]
return (cW.clamp(min=0) @ l[idx].t() + cW.clamp(max=0) @ u[idx].t() + cb[:,None]).t()
def robust_bound_error(model, X, y, epsilon):
initial_bound = (X - epsilon, X + epsilon)
err = 0
for y0 in range(10):
C = -torch.eye(10).to(device)
C[y0,:] += 1
err += (interval_based_bound(model, C, bounds, y==y0).min(dim=1)[0] < 0).sum().item()
return err
def epoch_robust_bound(loader, model, epsilon):
total_err = 0
C = [-torch.eye(10).to(device) for _ in range(10)]
for y0 in range(10):
C[y0][y0,:] += 1
for X,y in loader:
X,y = X.to(device), y.to(device)
initial_bound = (X - epsilon, X + epsilon)
bounds = bound_propagation(model, initial_bound)
for y0 in range(10):
lower_bound = interval_based_bound(model, C[y0], bounds, y==y0)
total_err += (lower_bound.min(dim=1)[0] < 0).sum().item()
return total_err / len(loader.dataset)
不像之前我们只是经验地去验证(即仅验证一些攻击样本的结果),现在我们尝试使用此边界来验证经过稳健训练后的模型是否能在某些情况下抵抗攻击。
epoch_robust_err(test_loader, model_cnn_robust, 0.1)
1.0
很不幸,该边界对于我们的我们的模型来说毫无意义(即界太大了,虽然结果表明误差是100%,但这没有意义)。需要说明的是,若想使用这种方法来验证,我们需要$\epsilon$的值小于$0.001$。因此我们尝试更小的$\epsilon$,如$\epsilon = 0.0001$,这样得到的结果才“合理”。
epoch_robust_err(test_loader, model_cnn_robust, 0.0001)
0.0261
这似乎并不是特别有用(因为$\epsilon$实在太小了),这实际上是所有基于松弛的验证方法的一个特性,即当用它们去评估一个我们不了解其边界的网络时,通常没什么意义的。此外,边界的误差还会随着网络的深度而累积,因为区间边界会逐层变得越来越松(这也是在上一章中我们将其用于三层神经网络,结果并不那么糟糕的原因)。
使用可证明的判据进行训练
如果用来验证的边界这么松弛,那它们的有什么意义呢?事实证明,如果我们专门根据此上界去最小化损失,那么我们会得到一个边界有意义的网络。
为此,我们将使用区间界来约束交叉熵损失的上界,并最小化该上界。具体的,如果我们令输出向量每一位上的值都替换成负数的对抗攻击目标值,并计算该向量的交叉熵损失,那么它将是原始损失的严格上界。
def epoch_robust_bound(loader, model, epsilon, opt=None):
total_err = 0
total_loss = 0
C = [-torch.eye(10).to(device) for _ in range(10)]
for y0 in range(10):
C[y0][y0,:] += 1
for X,y in loader:
X,y = X.to(device), y.to(device)
initial_bound = (X - epsilon, X + epsilon)
bounds = bound_propagation(model, initial_bound)
loss = 0
for y0 in range(10):
if sum(y==y0) > 0:
lower_bound = interval_based_bound(model, C[y0], bounds, y==y0)
loss += nn.CrossEntropyLoss(reduction='sum')(-lower_bound, y[y==y0]) / X.shape[0]
total_err += (lower_bound.min(dim=1)[0] < 0).sum().item()
total_loss += loss.item() * X.shape[0]
#print(loss.item())
if opt:
opt.zero_grad()
loss.backward()
opt.step()
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
最后,我们利用该稳健损失的界来训练模型。需要注意的是,通过这种方法训练稳健模型很有技巧性。如果上来就直接在$\epsilon=0.1$下训练稳健边界,那么模型将崩溃,把所有的类别预测为等概率。相反,我们需要从很小的$\epsilon$开始训练,并逐步将其增加到我们希望的水平。下面的代码中,我们使用的是随机选择,基本满足了我们的需要,如果微调一下的话效果会更好。
torch.manual_seed(0)
model_cnn_robust_2 = nn.Sequential(nn.Conv2d(1, 32, 3, padding=1, stride=2), nn.ReLU(),
nn.Conv2d(32, 32, 3, padding=1, ), nn.ReLU(),
nn.Conv2d(32, 64, 3, padding=1), nn.ReLU(),
nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU(),
Flatten(),
nn.Linear(7*7*64, 100), nn.ReLU(),
nn.Linear(100, 10)).to(device)
opt = optim.SGD(model_cnn_robust_2.parameters(), lr=1e-1)
eps_schedule = [0.0, 0.0001, 0.001, 0.01, 0.01, 0.05, 0.05, 0.05, 0.05, 0.05] + 15*[0.1]
print("Train Eps", "Train Loss*", "Test Err", "Test Robust Err", sep="\t")
for t in range(len(eps_schedule)):
train_err, train_loss = epoch_robust_bound(train_loader, model_cnn_robust_2, eps_schedule[t], opt)
test_err, test_loss = epoch(test_loader, model_cnn_robust_2)
adv_err, adv_loss = epoch_robust_bound(test_loader, model_cnn_robust_2, 0.1)
#if t == 4:
# for param_group in opt.param_groups:
# param_group["lr"] = 1e-2
print(*("{:.6f}".format(i) for i in (eps_schedule[t], train_loss, test_err, adv_err)), sep="\t")
torch.save(model_cnn_robust_2.state_dict(), "model_cnn_robust_2.pt")
Train Eps Train Loss* Test Err Test Robust Err
0.000000 0.829700 0.033800 1.000000
0.000100 0.126095 0.022200 1.000000
0.001000 0.119049 0.021500 1.000000
0.010000 0.227829 0.019100 1.000000
0.010000 0.129322 0.022900 1.000000
0.050000 1.716497 0.162200 0.828500
0.050000 0.744732 0.092100 0.625100
0.050000 0.486411 0.073800 0.309600
0.050000 0.393822 0.068100 0.197800
0.050000 0.345183 0.057100 0.169200
0.100000 0.493925 0.068400 0.129900
0.100000 0.444281 0.067200 0.122300
0.100000 0.419961 0.063300 0.117400
0.100000 0.406877 0.061300 0.114700
0.100000 0.401603 0.061500 0.116400
0.100000 0.387260 0.059600 0.111100
0.100000 0.383182 0.059400 0.108500
0.100000 0.375468 0.057900 0.107200
0.100000 0.369453 0.056800 0.107000
0.100000 0.365821 0.061300 0.116300
0.100000 0.359339 0.053600 0.104200
0.100000 0.358043 0.053000 0.097500
0.100000 0.354643 0.055700 0.101500
0.100000 0.352465 0.053500 0.096800
0.100000 0.348765 0.051500 0.096700
结果并没有刷新什么记录,不过我们可以说的是,对于这个分类器,以$\epsilon=0.1$的$\ell_\infty$攻击将不会使模型在MNIST测试集上出现超过9.67%的误差(标准误差是5.15%)。那么其对抗攻击的结果到底能有多差?这当然也很难说。不过我们可以看看PGD在其上的结果。
print("PGD, 40 iter: ", epoch_adversarial(test_loader, model_cnn_robust_2, pgd_linf, num_iter=40)[0])
PGD, 40 iter: 0.0779
不高不低。还需要注意的是,训练这种可证明稳健模型是具有挑战性的任务,一点点的微调都可以获得更好一些的效果。不过就我们的目的来说,目前这些内容足以表明可以通过有价值可证边界来训练模型。
前路漫长(又名:MNIST之外)
这里的内容也许会让你相信稳健模型似乎与与之相应的标准模型非常接近。然而,尽管我们希望这些内容能让你对这些方法的潜力感到兴奋,但需要强调的是,在大规模问题上构建与标准模型性能相当的稳健模型还有差得非常远。不幸的是,上述的这些模型看起来很有优势其实是源于我们使用的是MNIST数据集,在这类数据上创建稳健模型特别容易。
例如,即使是在CIFAR10这样的数据集上,最好的稳健模型也只能在$8/255=0.031$的扰动下达到55%的稳健误差,且最好的可证明稳健模型的误差大于70%。另一方面,在稳健优化中,训练方式、网络结构、正则化等等可选择的内容几乎都没有被涉及。我们所选的结构都是针对标准训练的最佳选择,但这些结构可能不是稳健训练的最佳结构。最后,正如我们在下一章中将要强调的那样,即使真正的稳健性难以捉摸,也能从现有的稳健模型中获得实质性的好处。