深度学习中的注意力机制/Attention Mechanism

沿着注意力机制的发展脉络，选取了三篇论文作一总结

背景

一切都要从Seq2Seq模型说起。

Seq2Seq模型（Sutskever, et al. 2014）最初是为机器翻译而提出。它使用LSTM将输入序列编码为一个定长向量，然后使用另一个LSTM从该向量中解码出目标序列，在形式上表现为encoder-decoder的结构。
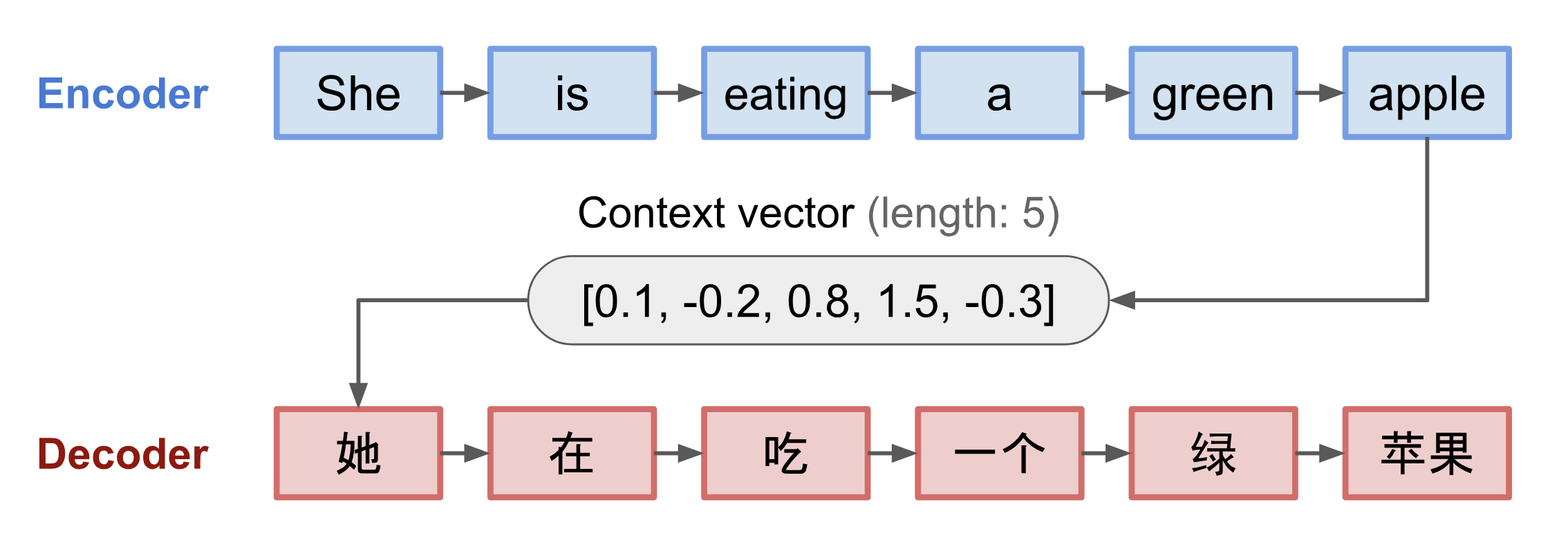
图1 Seq2Seq模型用于机器翻译的示例。图片来源：Lilian’s Blog

但是Seq2Seq模型的问题在于，它试图将整个句子压缩为一个向量表示，因此一旦句子过长，压缩向量就会“记不住”那么长的句子，导致模型的效果随着句子长度的增加而急剧变差。

注意力机制的提出

针对Seq2Seq模型的问题， Bahdanau等人第一次提出了注意力机制（Bahdanau et al., 2015）。有别于Seq2Seq模型将整个句子压缩为一个向量再去解码的做法，注意力机制的核心是使用上下文向量（context vector）来生成输出序列。其中上下文向量基于encoder和decoder的隐向量（hidden state）得到。

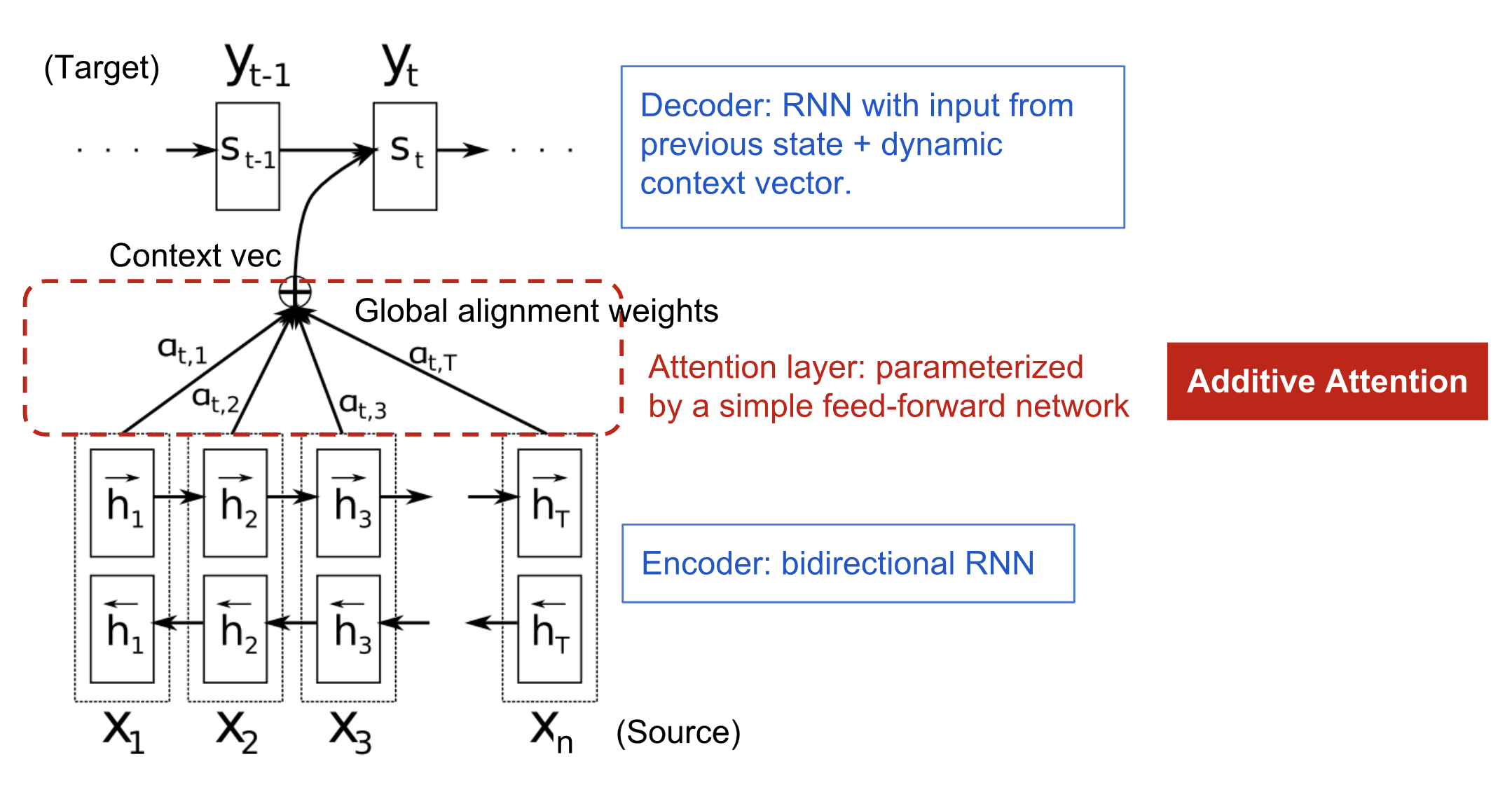
图2 Bahdanau et al., 2015使用的模型结构
首先，decoder的输出是联合条件概率模型： $p(\mathbf{y})=\prod_{t=1}^{T} p\left(y_{t} |\left\{y_{1}, \cdots, y_{t-1}\right\}, c_{t}\right) \tag{1.1}$ 其中，$\mathbf{y}=\left(y_{1}, \cdots, y_{T_y}\right)$是输出的句子，$c_{t}$是上下文向量。联合条件概率中的每一个条件概率可以被建模成为： $p\left(y_{i} |\left\{y_{1}, \cdots, y_{i-1}\right\}, c_{i}\right)=g\left(y_{i-1}, s_{i}, c_{i}\right) \tag{1.2}$ 其中$g$是非线性函数，用来输出单词$y_t$的作为结果的概率，$s_t$则是decoder RNN的隐向量： $s_{i}=f\left(s_{i-1}, y_{i-1}, c_{i}\right) \tag{1.3}$

上下文向量$c_{i}$是encoder中所有隐向量$h$的加权和： $c_{i}=\sum_{j=1}^{T_{x}} \alpha_{i j} h_{j} \tag{1.4}$

每个隐向量$h_j$的权重$\alpha_{i j}$通过softmax计算而得： $\alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)} \tag{1.5}$ 其中 $e_{i j}=a\left(s_{i-1}, h_{j}\right) \tag{1.6}$ 这里的$a$是一个前向传播神经网络，用来计算在位置$j$附近的输入序列和在位置$i$附近的输出序列的匹配程度。

从公式$(1.4)$中可以看出，由于上下文向量$c$用到了整个输入序列，因此就解决了因句子过长导致的遗忘问题。概率$\alpha_{i j}$反映的是隐向量$h_j$对于决定下一个状态$s_i$并生成$y_i$的重要程度，也正是在这里体现了“注意力”，即decoder只需要“注意”输入序列中的某一部分——不太重要的部分权重小一点，重要的部分权重大一点。通过这一注意力机制，encoder便不再需要将整个长句的信息压缩到一个定长向量中。

全局 vs 局部注意力/Global vs Local attention

紧接着，Luong, et al., 2015提出了“全局（Global）”和“局部（Local）”注意力。
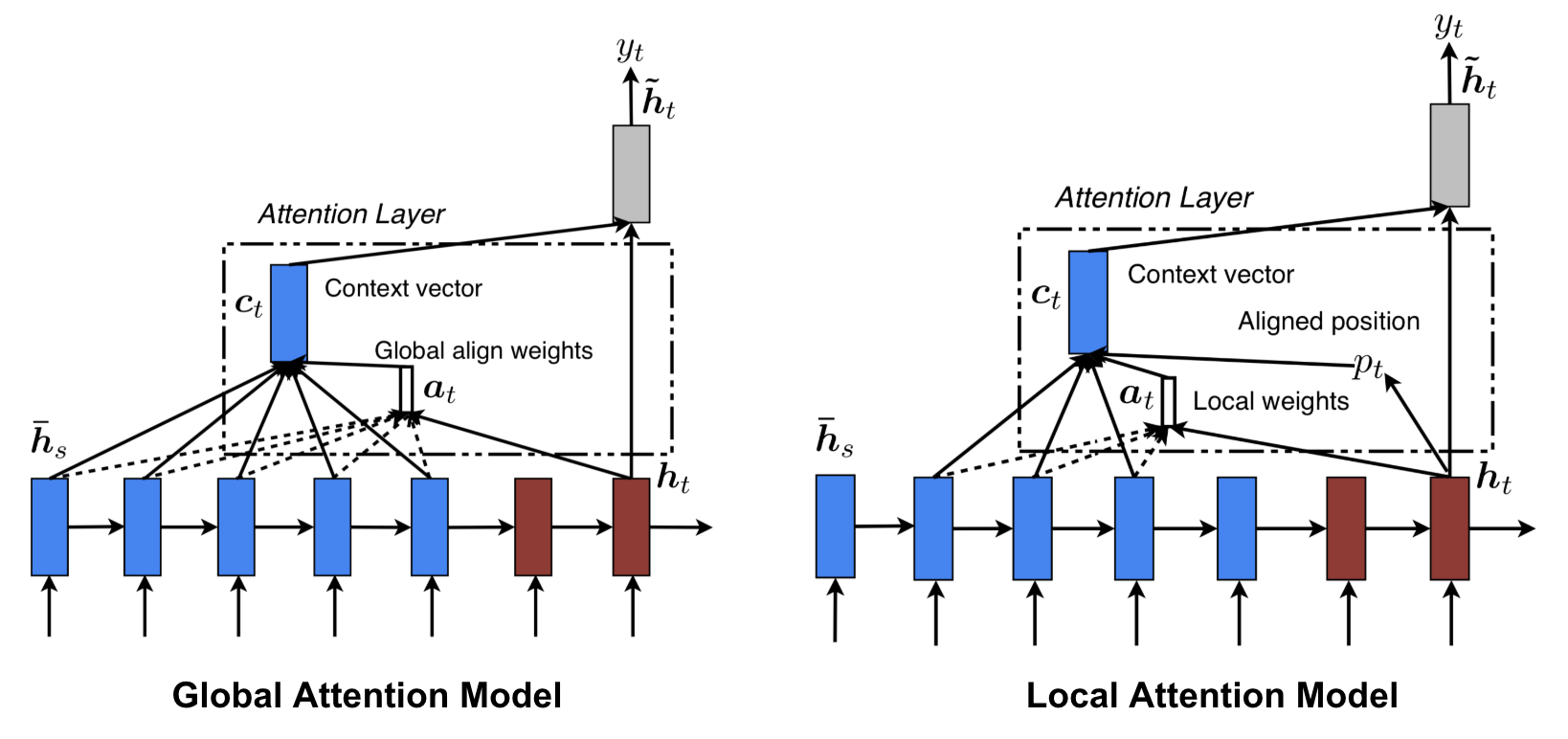
图3 全局和局部注意力机制示意图

Global attention 和Bahdanau et al., 2015中的方法很相似，但做了如下改动：
1. encoder使用了单向RNN，而Bahdanau et al., 2015使用的是双向RNN。这样做的好处是省去了组合两个方向上隐向量的工作；
2. Luong, et al., 2015的计算顺序是$h_t\rightarrow a_t\rightarrow c_t\rightarrow \tilde{h}_t\rightarrow y_t$，即decoder的隐向量是按照常规RNN的方法计算得到的，$e.g.,\ h_t=tanh(W_{hh}h_{t-1}+W_{xh}x_t)$，再去计算上下文向量$c_t$，然后将$h_t$和$c_t$级联到一起作为所谓的注意力隐向量(attentional hidden state) $\tilde{h}_t$，$\tilde{h}_t$被用于预测$p\left(y_{t} \mid y_{<t}, x\right)=\operatorname{softmax}\left(\boldsymbol{W}_{s} \tilde{\boldsymbol{h}}_{t}\right)$；而Bahdanau et al., 2015是用上一步的隐向量计算出上下文向量后，再在此基础上计算当前步的隐向量$h_{t-1}\rightarrow a_t\rightarrow c_t\rightarrow h_t\rightarrow y_t$。换言之，Luong, et al., 2015在计算预测结果时用到上下文向量，而Bahdanau et al., 2015在计算decoder的隐向量时用到上下文向量，两者的逻辑顺序有些许不同。
3. 提出了多种方法来计算注意力的权重。
  
  具体来说：
  $h_t\rightarrow a_t$，即利用decoder和encoder的隐向量计算权重向量：
  \[\begin{aligned} \boldsymbol{a}_{t}(s) &=\operatorname{align}\left(\boldsymbol{h}_{t}, \overline{\boldsymbol{h}}_{s}\right) \\ &=\frac{\exp \left(\operatorname{score}\left(\boldsymbol{h}_{t}, \overline{\boldsymbol{h}}_{s}\right)\right)}{\sum_{s^{\prime}} \exp \left(\operatorname{score}\left(\boldsymbol{h}_{t}, \overline{\boldsymbol{h}}_{s^{\prime}}\right)\right)} \end{aligned}\]
  这一步与Bahdanau et al., 2015在方式上没有区别，都是使用了softmax。唯一的不同之处是Bahdanau et al., 2015使用的是$h_{t-1}$。（其中$\overline{\boldsymbol{h}}_{s}$是encoder的隐向量）
  $a_t\rightarrow c_t$，即利用权重向量和encoder的隐向量计算上下文向量：这一步没什么意外，向量做内积即可。
  $c_t\rightarrow\tilde{h}_t\rightarrow y_t$，即利用上下文向量计算注意力隐向量$\tilde{\boldsymbol{h}}_{t}$和预测输出$p\left(y_{t} | y_{\lt t}, x\right)$
  \[\begin{aligned}&\tilde{\boldsymbol{h}}_{t}=\tanh \left(\boldsymbol{W}_{c}\left[\boldsymbol{c}_{t} ; \boldsymbol{h}_{t}\right]\right) \\ &p\left(y_{t} | y_{\lt t}, x\right)=\operatorname{softmax}\left(\boldsymbol{W}_{s}\tilde{\boldsymbol{h}}_{t}\right) \end{aligned}\]
Local attention：然而Global attention的一个缺陷是，在计算每个输出时都用到了encoder中的所有词语。一旦句子过长，例如段落或是文章，那么这种方法就会显得非常低效。因此Luong, et al., 2015接着提出了Local attention，只使用源语句中的部分词语产生输出。其灵感的来源是Xu et al. 2015针对图像领域提出的soft & hard attention。

具体来说，Local attention首先为$t$时刻的输出目标在源语句中预测出一个匹配位置$p_t$（aligned position），并以$p_t$为中心选定一个窗口$\left[p_{t}-D, p_{t}+D\right]$，其中$D$是超参数。上下文向量$c_t$仅通过该窗口内encoder的隐向量的加权和计算而得。 $p_{t}=S \cdot \operatorname{sigmoid}\left(\boldsymbol{v}_{p}^{\top} \tanh \left(\boldsymbol{W}_{\boldsymbol{p}} \boldsymbol{h}_{t}\right)\right)$

$\boldsymbol{W}_{\boldsymbol{p}}$和$\boldsymbol{v}_{p}^{\top}$都是模型参数，$S$是源语句的长度。为了使得更靠近中心的词语的权重更大，又引入了高斯分布为系数来对权重做修正：

\[\boldsymbol{a}_{t}(s)=\operatorname{align}\left(\boldsymbol{h}_{t}, \overline{\boldsymbol{h}}_{s}\right) \exp \left(-\frac{\left(s-p_{t}\right)^{2}}{2 \sigma^{2}}\right)\]

Transformer

上述方法都不约而同地使用RNN来完成Seq2Seq的任务，这是基于RNN处理序列数据的天然优势。然而，这种优势同时也不幸成为了阻碍RNN在训练过程中并行化的绊脚石。一旦序列过长，有限的内存将会限制样本的批处理。“Attention is All you Need”(Vaswani, et al., 2017)提出的transformer模型毫无疑问是第一个只靠self-attention而不使用RNN计算句子输入输出表示的方法。

Vaswani, et al., 2017文中对self-attention的解释仅有一句”所谓的self-attention，又名intra-attention，是一种关联句子中不同位置上的词语来计算句子表示的注意力机制。”，这让第一次接触这个概念的人难免看得云里雾里。经我查阅资料后，目前对此的理解就是一种，不同于RNN那样将源语句依次嵌入成隐向量实现信息融合，而是同时基于源语句中的词语去计算attention。简言之，就是要用前馈神经网络去完成之前RNN做的事。
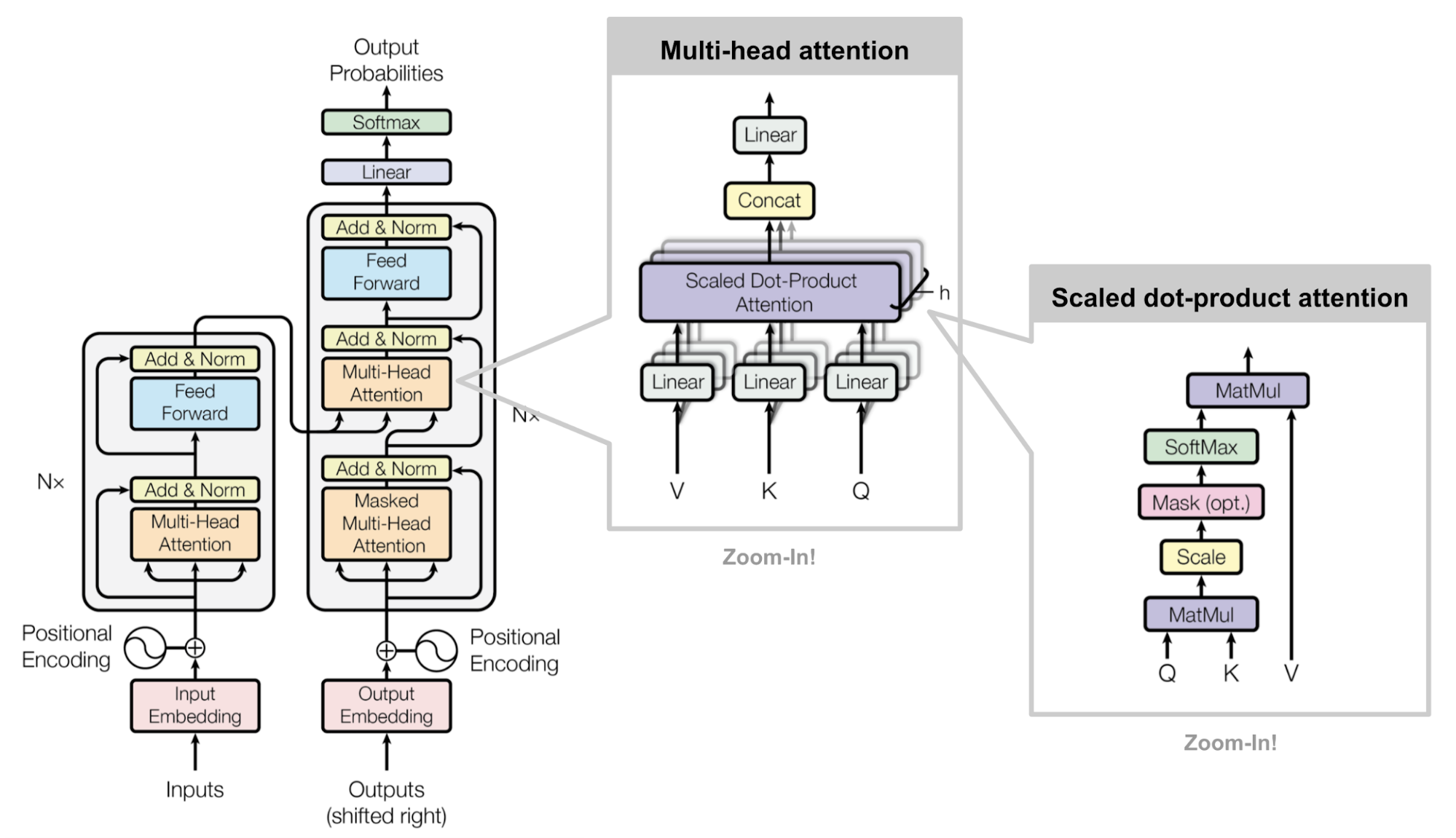
图4 Transformer的框架

Scale dot-product attention

Scale dot-product attention就是上图中最右侧的子图所示。
看多了之前的RNN模型，很容易在此处产生误解。尤其是看到了encoder-decoder的结构，以及下面提到的attention计算公式，会不自觉地想要将transformer和基于RNN的模型对应起来。所以建议直接将这里的设定当做是全新引入的来接受。
首先出现的是三个输入向量，分别是query(Q)、key(K)、value(V)，它们都是由词向量乘以不同的参数矩阵后得到。（在input embedding中完成对词语的向量化，其中key和value作为一对，其维度是相同的），如下图所示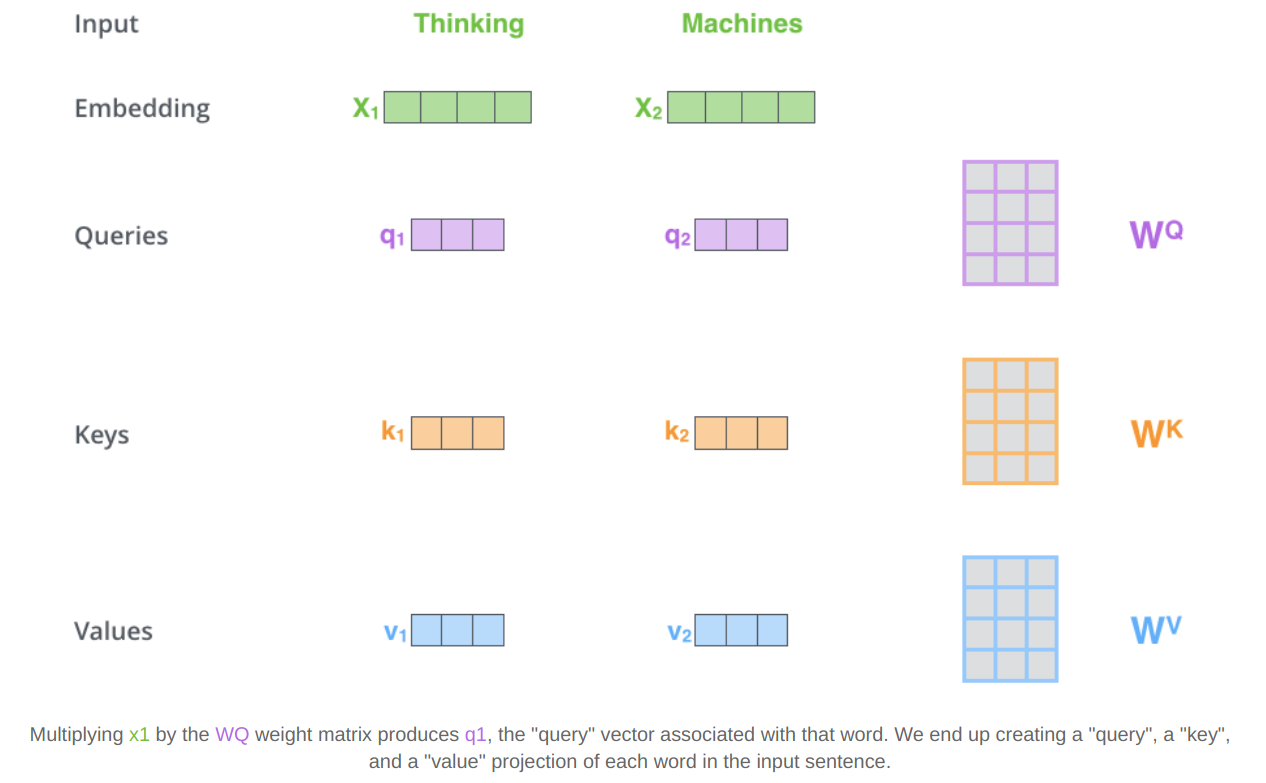：清楚了输入向量之后，我们直接来看attention的计算： $\text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V$ 这里就和上述基于RNN的模型有些相似了。因为计算attention所需的信息是共享的，即(K，V)，所以此处的Q表示多个query构成的矩阵，通过矩阵相乘一并快速计算。（ps：”scale”体现在公式中除以$\sqrt{d_k}$）

Multi-Head Self-Attention

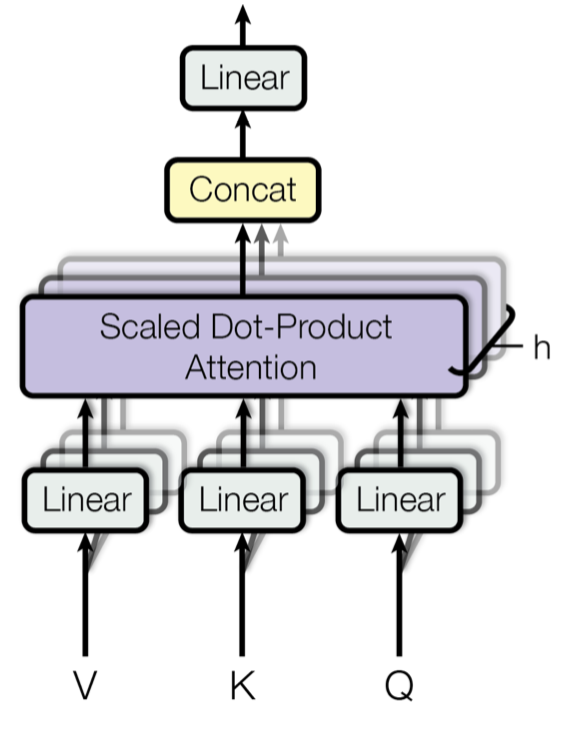
图5 Multi-head scaled dot-product attention mechanism. (图像来源: Fig 2 in Vaswani, et al., 2017)

上述的Scale dot-product attention是一次性计算attention，而Multi-Head Self-Attention则是多次并行计算attention。具体来说：

首先利用一组参数矩阵$W^Q,W^K,W^V$对$Q,K,V$三个矩阵分别做线性变换，然后再接Scale dot-product attention。线性变化的目的是降维，比如Vaswani, et al., 2017文中就将维度从512将至64。由此得到的结果称为$head$；
一共有$h$组经过不同初始化得到的参数矩阵$W^{Q}_i,W^{K}_i,W^{V}_i$，每一组都做同样的Scale dot-product attention，于是得到$h$组$head$，然后将它们级联到一起后再做一次线性变换。
\[\begin{aligned} \text { MultiHead }(Q, K, V) &=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}} &=\text { Attention }\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}\]

这里再用一张图示意上述流程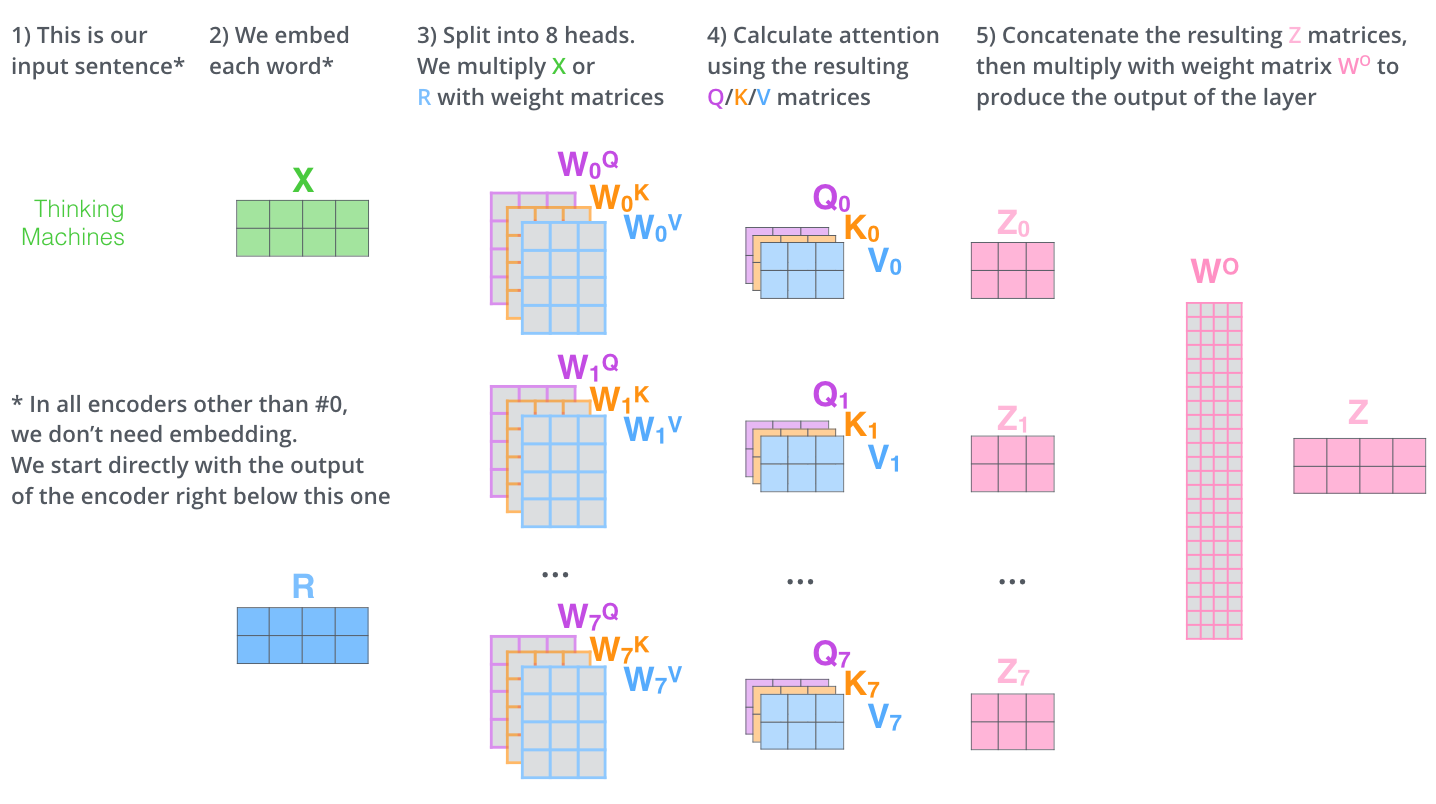：文中说这样做的好处是attention联合了不同的表示子空间，而single-head attention则相当于取了它们的平均。而且文中说这样做和原先的single-head attention相比计算量差不多。

Positional Encoding

毕竟语句是序列数据，词语的顺序也是至关重要的信息。transformer使用Positional Encoding来引入顺序的信息。简单来说就是给input embedding加上一个向量，而这个向量可以在一定程度上反映词语在句子中的位置信息。文中是使用正弦函数和余弦函数来完成这一步的，想了解细节还请参考原文。

从encoder到decoder

从encoder最上层的那个模块到decoder模块的中间层输入其实还是遵循了之前的做法，即通过参数矩阵对encoder的输出做线性变换，得到一组（K，V），而Q则来自与decoder模块的第一层的输出。

decoder

和encoder的模块稍有不同，decoder的模块中包含了三个子层，其中第二层和第三层与encoder无异，而第一层略微改变的地方是使用了Masked Multi-Head Attention。具体来说，在解码器中仅允许self-attention关注输出序列中“过去”的位置。这是通过在self-attention计算softmax步骤之前，先屏蔽掉“将来”的位置（将它们设置为-inf）来完成的。