CS231n看过已有半年之久,当时花费不少时间在iPad上手写了大量笔记。昨日读论文时翻看笔记复习了优化方法这一部分,突然觉得差不多也该整理整理这些笔记了。一方面是因为这门课的质量确实高,另一方面也希望通过整理笔记的过程把这些知识再温习一遍。本文对神经网络中常见的优化方法做一梳理。
因为梯度下降(gradient descent)过于基础,严格来讲应该是高数的内容,所以我们直接从SGD开始整理吧。
1. SGD
随机梯度下降(SGD)相比于朴素的梯度下降,最大的差别就是多了“随机”两个字……先别打我,事实的确是这样。“随机”体现在每一轮用来更新参数的数据只是从整体数据集中“随机”挑选出的一部分,然后再做梯度下降:
while True:
weight_grad = evaluate_grad(loss_function, data, weights)
weights += -stepsize * weight_grad
它相比于梯度下降的优势是不需要在整个数据集上计算梯度后才更新参数,因而效率更高。但SGD有如下三个问题:
-
条件数问题
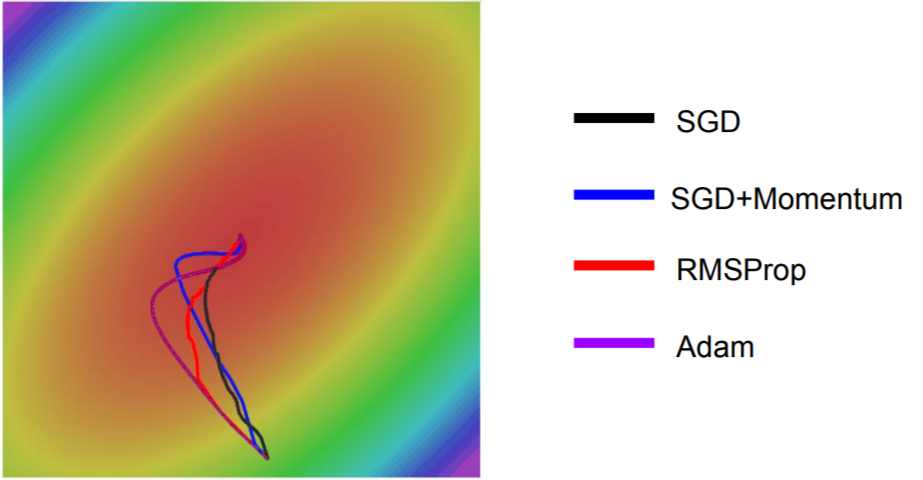
如果loss在一个方向上变化过快(梯度大),而在另一个方向上变化缓慢(梯度小),那么就会表现出图中锯齿状更新路径:
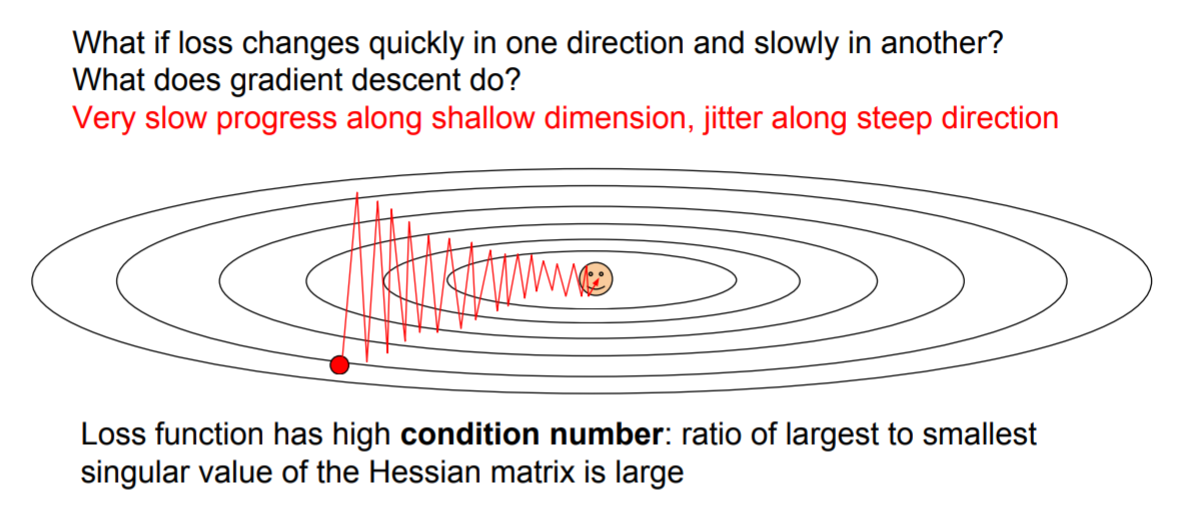
回到那个用来解释梯度下降的经典例子中——下山,就能很好地理解这一点:理想的情况是沿着最陡的方向下降,但如果这时候存在一个水平方向的速度,而且这个速度还很快,那就变成沿着螺旋线盘旋下山了——需要花更长的时间才能到达山脚。上图演示的还只是2个参数的情形,当有上百万个参数时,最大和最小的参数变化率的差异巨大,会使得SGD的表现很差。
-
陷入鞍点
当只有几个参数时,可以很容易理解陷入鞍点的情况:各个参数在某点处的一阶导数为零且二阶导数同号。此时虽然一阶导数为零,优化停止,但明显连局部最优都算不上。但当参数量是上百万时,鞍点会成为一个大问题。 以10个参数为例,当某点是各个参数的驻点时,它是局部最优点的概率为$2×0.5^{10}$,而它是鞍点的概率则是$1-2×0.5^{10}$!也就是说,当用SGD优化停止时(一阶导数为0,更新停止),参数更有可能是陷入到了鞍点而非局部最优点。此外问题还会出现在鞍点附近,在接近鞍点的地方梯度会变得非常小,因此参数更新会非常缓慢。
-
“随机”
理想的情况是将所有样本一次性输入计算loss,但由于样本总量太大,这样做并不现实。故输入的是一个mini batch的样本,但这意味着得到的并非真正的梯度,而是对真实梯度的一个估计(课程中称之为noisy gradient),所以实际的更新过程会变得缓慢。
幸运的是,SGD+momentum可以解决上述问题。
2. SGD+momentum
核心思想是在更新时引入一个速度,此时不再沿梯度方向更新,而是沿速度方向更新。其中$\rho$是衰减因子:
\[\begin{array}{l} v_{t+1}=\rho v_{t}-\nabla f(x_{t})\\ x_{t+1}=x_{t}+\alpha v_{t+1} \end{array}\]它的好处在于:
- 对于条件数问题,在没有引入速度前,更新路径为锯齿状;但有了速度之后,就有可能抵消各个参数间的变化差异。这里的解释是,梯度变化敏感的那个方向上因为有了上一次的速度,“惯性”会使得其“调头”变得困难;同时,梯度变化迟缓的那个方向上则会一直加速。
- 对于陷入鞍点的问题,当遇到局部最优点或鞍点时,由于具有上一次的“速度”,即使此处的梯度为零,仍可以通过顺利通过。
- 关于noisy gradient的问题,由于引入了速度,使更新路径更加平缓,这在一定程度上缓解了“噪声”。此外,从更新公式中可以看出,速度不断地衰减并与梯度累加(初始速度为零),所以不妨把速度看做是之前所有梯度(各个方向上)的折衷,故更新路径更加平滑。
3. Nesterov Momentum
\[\begin{array}{l} v_{t+1}=\rho v_{t}-\alpha \nabla f(x_{t}+\rho v_{t}) \\ x_{t+1}=x_{t}+v_{t+1} \end{array}\]Nesterov Momentum与SGD+momentum相比最大区别在于,计算梯度的位置$(x_t+\rho v_t)$和实际更新的位置$(x_t)$不同。这么操作乍一看难免让人有点难以理解,为此我们将\(\tilde{x}=x_t+\rho v_t\)代入上式:
\[\begin{split} v_{t+1}&=\rho v_t-\alpha \nabla f(\tilde{x_t})\\ x_{t+1}&=\tilde{x_t}-\rho v_t+(1+\rho)v_{t+1}\\ &=\tilde{x_t}+v_{t+1}+\rho (v_{t+1}-v_t) \end{split}\]如此一来,Nesterov Momentum就有了良好的解释——相比于SGD+momentum只是多了一项“速度差”。
定性的理解是:我们引入“速度”的目的是使优化过程可以顺利地通过驻点,也就是故意跑偏;但我们又不希望这个“速度”使更新方向跑偏得太离谱,毕竟计算出的(负)梯度方向才是下降最快的方向。最好的情况是在计算出的更新方向附近跑偏一点点就好。 从矢量图中可知,引入了“速度差”之后,实际的更新方向会更加偏向负梯度方向,于是“速度”的影响就被削弱了。
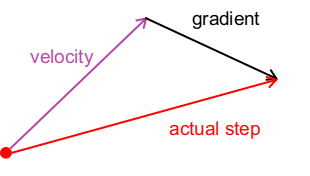
此外,Nesterov Momentum在凸优化问题中还有一些其它良好的理论性质。
4. AdaGrad
AdaGrad可以显著地解决条件数问题。
\[\begin{array}{l} sum=sum+\left(\nabla f(x_{t})\right)^2\\ x_{t+1}=x_{t}-\alpha·\frac{\nabla f(x_{t})}{\sqrt{sum}+1×10^{-7}} \end{array}\]从上式中可以明显地看到,AdaGrad会基于梯度每一维上的平方和,对梯度进行尺缩。这样,在梯度较大的方向上,相比于梯度较小的方向,其步长会逐渐减小。
但是AdaGrad的问题是,随着训练时间的增长,所有步长都会减至很小,使得更新停滞。这对于凸优化来说是件好事,因为在接近最优点时我们希望减速;但对于非凸优化来说,这一性质就不太友好了。
5. RMSProp
RMSProp是对AdaGrad的改进:
\[\begin{array}{l} sum=\rho·sum+(1-\rho)·\left(\nabla f(x_{t})\right)^2\\ x_{t+1}=x_{t}-\alpha·\frac{\nabla f(x_{t})}{\sqrt{sum}+1×10^{-7}} \end{array}\]神似于momentum之于SGD,只不过velocity变成了梯度的平方和。在保证解决条件数问题的基础上,又解决了步长一直减小的问题。
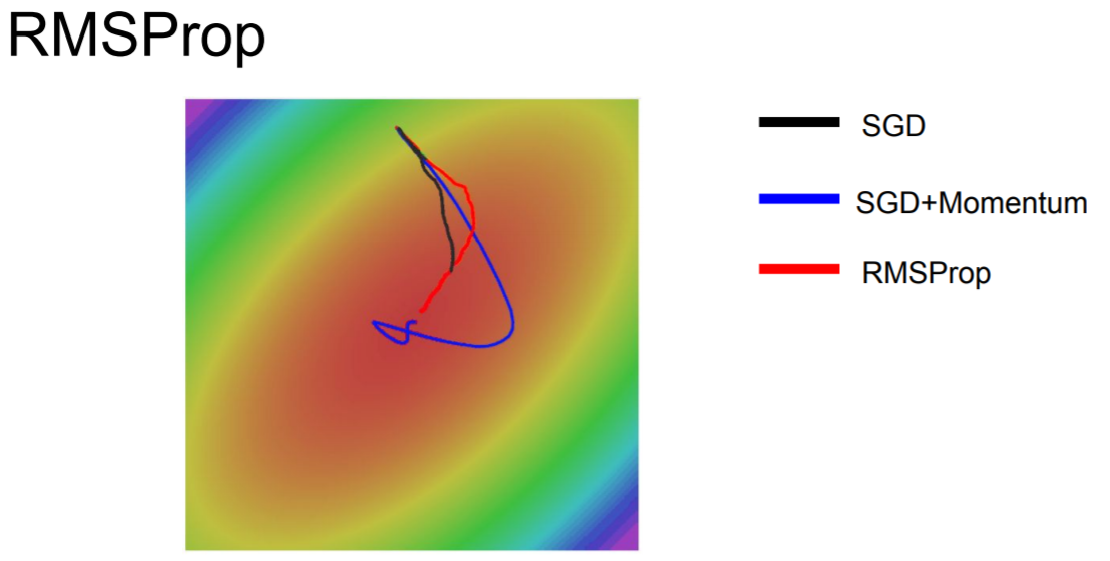
从上图可以看出,SGD+Momentum是冲过头了然后再慢慢调整回来,而RMSProp是在更新的过程中逐渐调整。
6. Adam (almost)
从上面的内容可以看出,引入速度(梯度偏移)可以改善陷入鞍点的问题,而AdaGrad和RMSProp通过放缩梯度来改善条件数的问题。那么何不将这两种技巧放在一起呢?这便是Adam的雏形:

但这里的问题是,在一开始更新时,因为second_moment初始化为0,且beta_2通常设置为0.9, 0.99之类的数,从而second_moment会很小,这使得一开始的步长会非常大,将更新带到了某个糟糕的地方。虽然second_moment会随着之后的优化而累积,更新会回到正轨,但这意味着前几轮的更新都是白费功夫!
7. Adam (full form)
通过引入修正机制来解决上述问题。
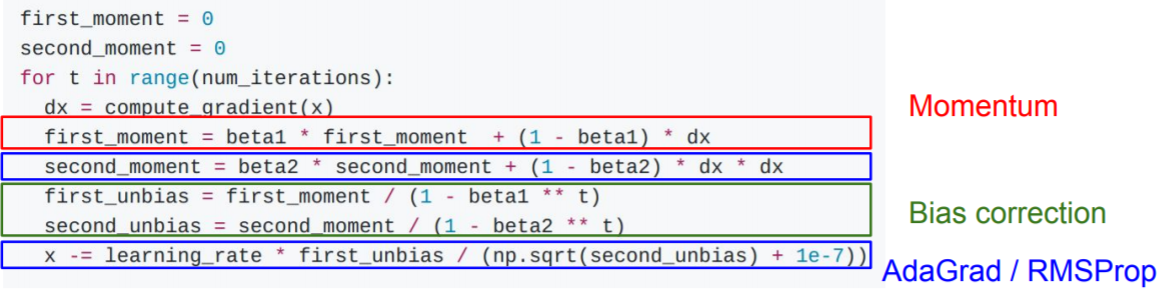
这样,前几轮的更新量就不会过小。
目前,Adam通常是深度学习实验中首选的优化方法,从下图中也可以看出,Adam综合了SGD+Momentum和RMSProp的优点。
8. 浅谈二阶优化方法
需要说明的是,上述的所有优化方法都是**一阶优化**,即利用了原函数的一阶泰勒展开式去近似表示原函数:
\[f(x) \approx f(x_0)+f^{\prime}(x_0)(x-x_0)\]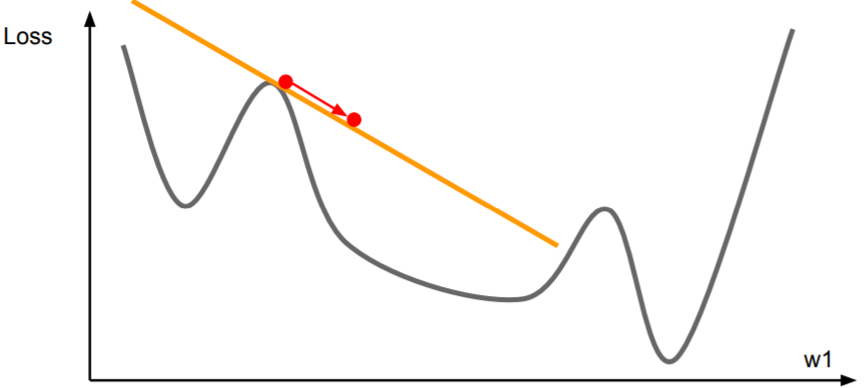
满足$(x-x_0)$与\(f^{\prime}(x_0)\)反号的$x$能够令$f(x)$减小。但一阶优化方法需要设置学习率。
现在考虑用二阶泰勒展开式来近似:
\[f(x) \approx f(x_0)+f^{\prime}(x_0)(x-x_0)+\frac{f^{\prime\prime}(x_0)}{2!}(x-x_0)^2\]如果写成二阶近似,就可以直接求出极值点,从而不再需要学习率!
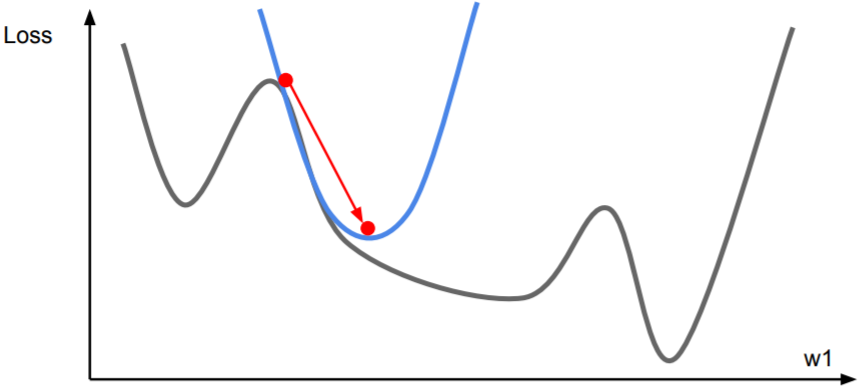
不过这样做的代价是需要为此计算Hessian矩阵的逆,而这对于深度学习来说是不现实的。假设参数量为$N$,那么Hessian矩阵的维度是$N×N$,可能内存中都不够放,求逆则更是复杂($O(N^3)$)。
因此实际中通常使用的是Hessian矩阵的近似。比较有名的算法是L-BFGS,对于full-batch训练很有效,但对mini-batch训练则很糟糕。