对VAE的理解一直都很模糊。由于打算用GAN来做实验,作为基础,有必要彻底把VAE弄懂。 回过头又把CS231n关于VAE的部分来回看了好几遍,说真的,Serena Yeung讲得比Justin小哥差太多了,实在没法理解。 所幸在网上找到了一篇博文,清晰明了。 博文里已经讲得很清楚了,我在此用自己的理解做一总结。
动机
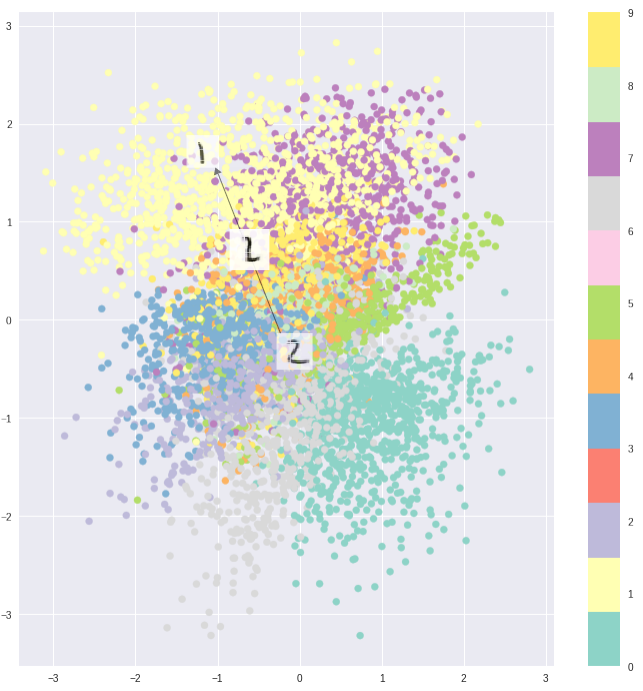
自编码器的缺点在于,不同类别的样本映射到特征空间后是不连续的。
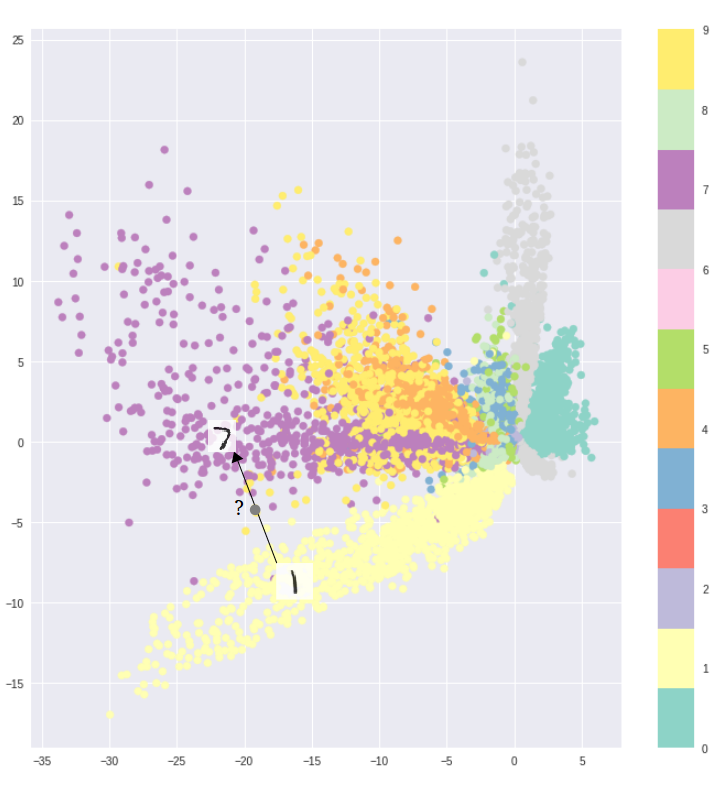
例如上图是在MNIST数据集上训练得到,可以看到不同类别的数字图像在二维空间中被明显地分开。它的好处仅表现在去区分和训练数据相似的数据。
但生成模型的目的是从潜在空间(latent space)中随机采样,或是在输入图像的基础上生成一些变体(要求潜在空间的连续性),从上图明显可以看出,潜在空间中还有大量没有被覆盖到的区域——如果在这些区域上采样,解码器该如何判断?
我们希望不同的类别彼此尽可能靠近同时又能区分开。 这就是VAE做的事情。
概率解释
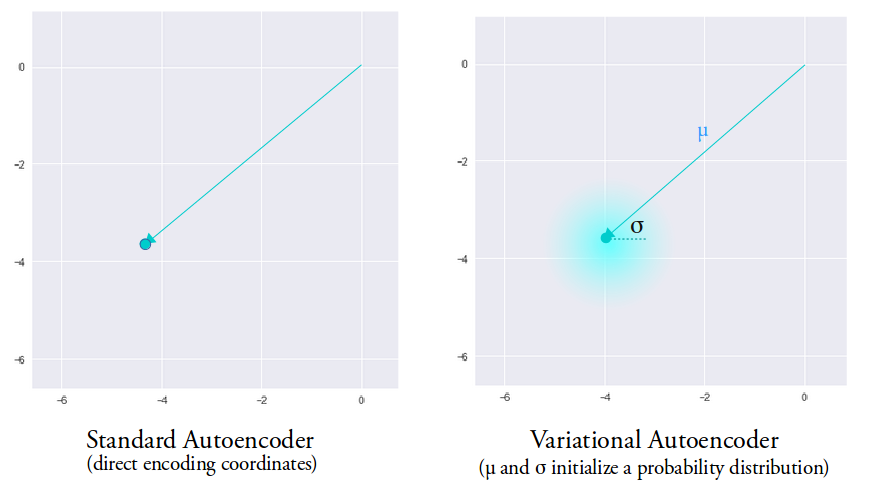
关于VAE我最大的疑惑就是encoder network的输出到底是什么。看到下面这张图后才豁然开朗:
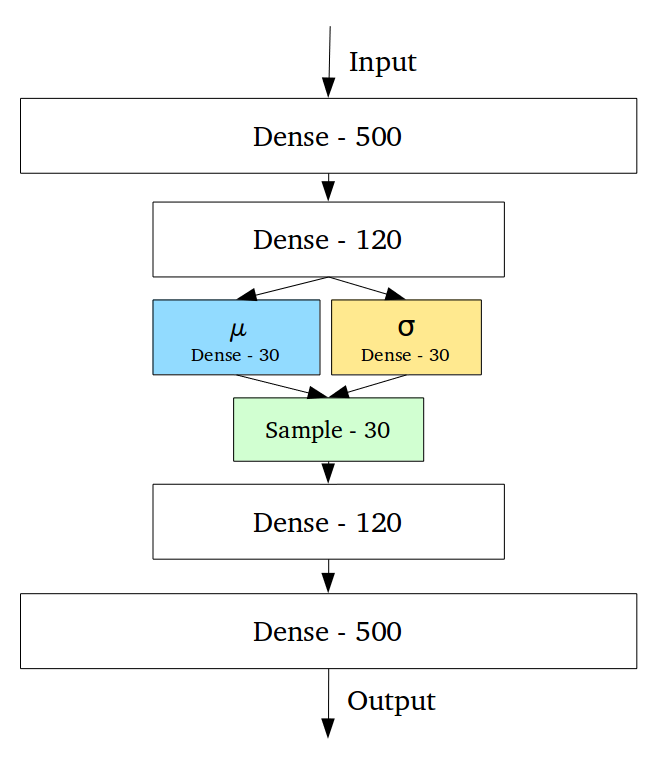
encoder network的输出的确是均值和方差,多维决定了这是多个随机变量,这才有了后面的多维高斯分布。 比如下图中均值和方差分别是30维,即30个随机变量,每组均值和方差都决定了一个高斯分布。从这些分布中采样即可得到$z$

从分布中采样的好处是,即使对于同一个输入$x$,encoder输出的$z$也可能不同。因为这是按概率在均值$\mu$和方差$\sigma$确定的一片区域内采样得到的。其意义是使decoder将潜在空间的这片区域对应到同一个类别,而不再是只将潜在空间的一个点对应某一类别。
损失函数
回到我们的目标——使不同类别的输入在潜在空间中既能彼此靠近又能互相区分。
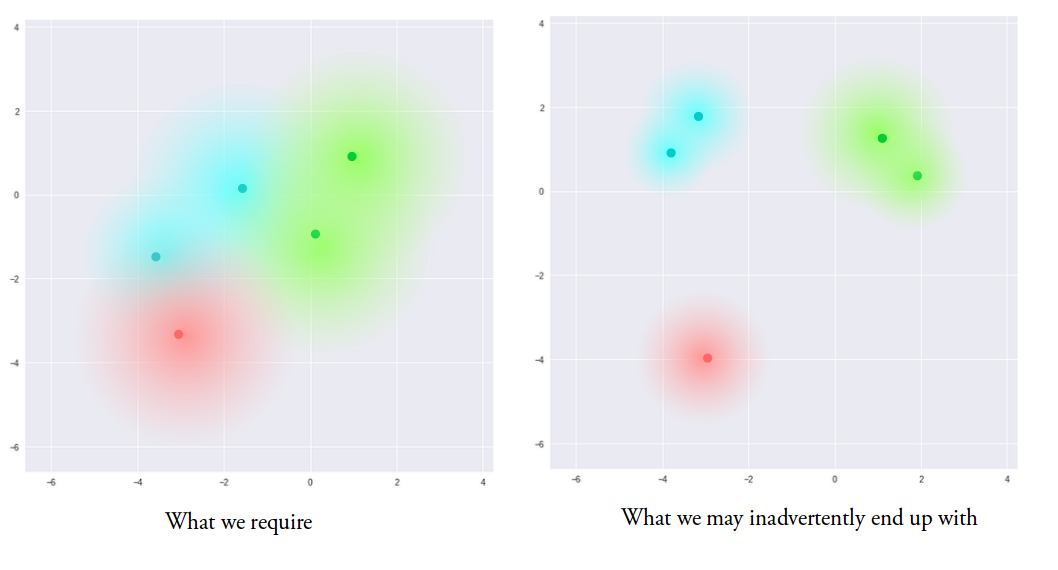
靠近:在没有约束的情况下,为了便于分类,encoder输出的$\mu$和$\sigma$会很分散。其后果就是不同随机变量的分布在潜在空间中“各自为王”。VAE的做法是让这些随机变量的分布都向标准正态分布靠近,偏离则会受到惩罚,其本质就是正则化。度量分布之间的距离选用的是KL散度。
但仅仅考虑靠近在一起是下图这样的效果:
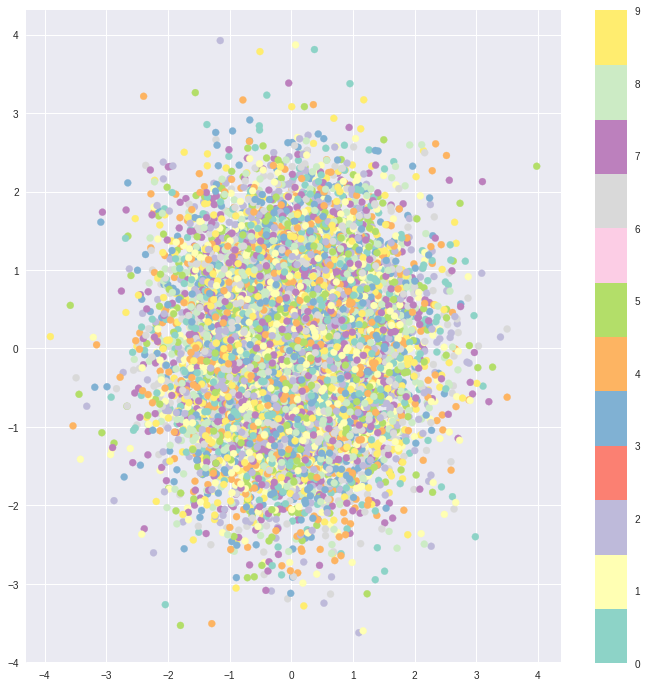
区分:靠decoder来完成。
最终的损失函数为: \(l_{i}(\theta, \phi)=-\mathbb{E}_{z \sim q_{\theta}\left(z | x_{i}\right)}\left[\log p_{\phi}\left(x_{i} | z\right)\right]+\mathbb{K} \mathbb{L}\left(q_{\theta}\left(z | x_{i}\right) \| p(z)\right)\) 第一项就是decoder网络的优化目标,是为了将不同类别在局部上区分;第二项是正则项,为了在全局上保持连续性。 值得一提的是,这个损失函数可不是拍脑袋想出来的,而是经由贝叶斯公式推导而得。喜人的是,可以对损失函数的项做出解释。
生成过程
生成数据时只用到了decoder网络,即$z$不再是从$q_{\phi}(z | x)$中采样,而是直接从标准正态分布中采样。因为$q_{\phi}(z | x)$只是为了训练decoder而引入的,目的是把样本数据集在潜在空间中聚拢,聚拢的目标是标准正态分布。经过训练后,decoder已经可以从这样的空间中区分不同类别的数据。生成时直接从标准正态分布采样$z$即可。