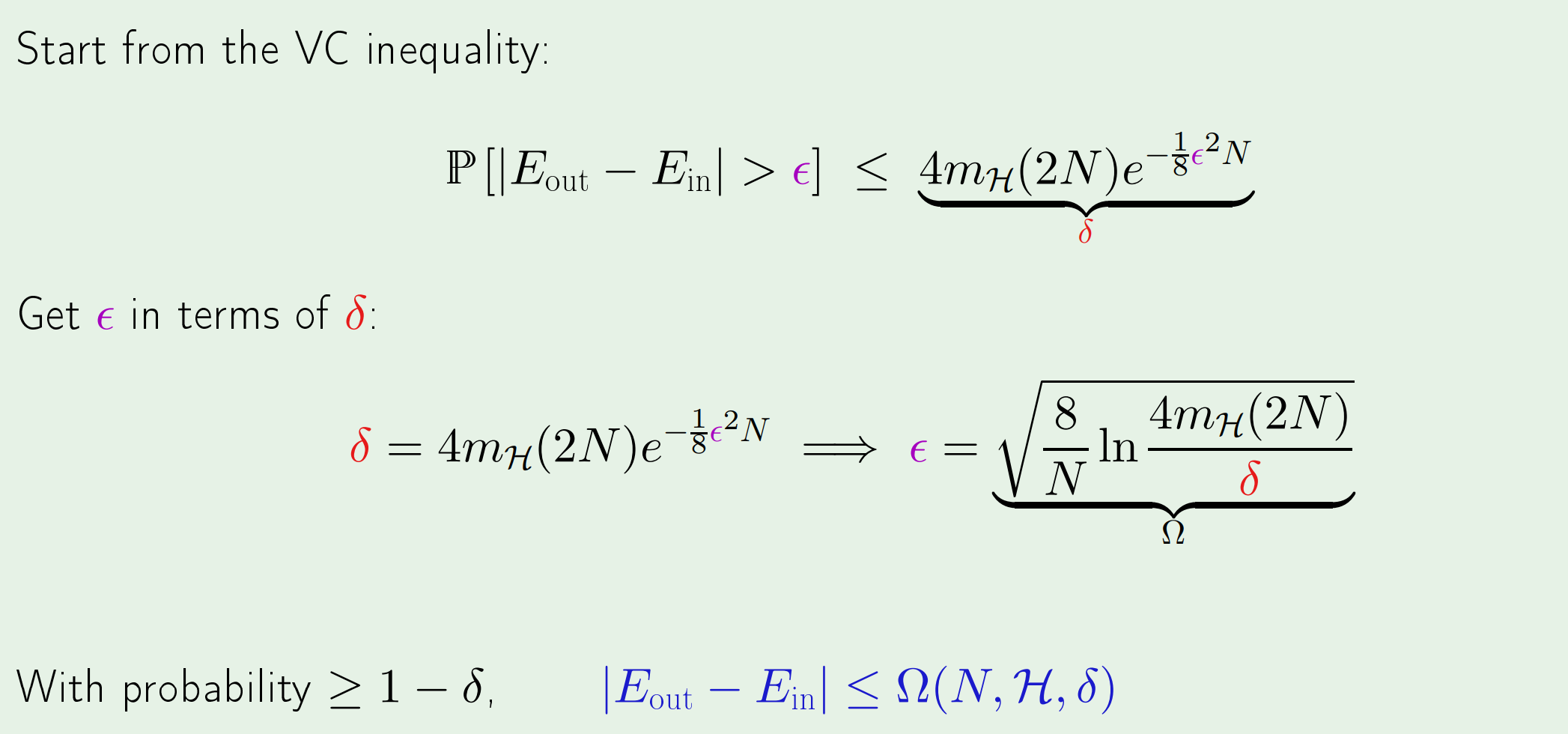我在夏季学期选修了《统计机器学习理论》,虽然课程只上了短短一周,但却令我耳目一新,越上越觉得有趣,捧起Vapnik那本《统计学习理论的本质》也看得津津有味。课程最后要求就自己感兴趣的部分写一份调研报告,在查阅资料的过程中偶然发现了Caltech的一门课:Learning From Data,前7课讲的恰好是统计学习理论。老爷子讲得很生动形象,强烈推荐。在此对这部分课程做一梳理总结。
前三课
前三课主要讨论了是否可学习的问题,答案是肯定的:learning is feasible。 这一回答的底气来自Hoeffding不等式。

如果仅存在一种hypothesis,那么可以直接由Hoeffding不等式得到经验误差和真实误差之间差距的上界。
但现实中的模型往往并不存在只有一种假设的情况,假设的数量通常是无限的。想要继续通过Hoeffding不等式来约束差距就会得到上图右半边的结果,即多了模型数量这一因子: \(\mathbb{P}\left[\left|E_{\mathrm{in}}-E_{\mathrm{out}}\right|>\epsilon\right] \leq 2 M e^{-2 \epsilon^{2} N}\)
虽然这个上界很可能是没有意义的(因为$M$通常是无穷大),但至少给出了一个上界,它告诉我们是可以学习的。
关于为什么要引入这么多假设,教授用形象的例子给了解释。
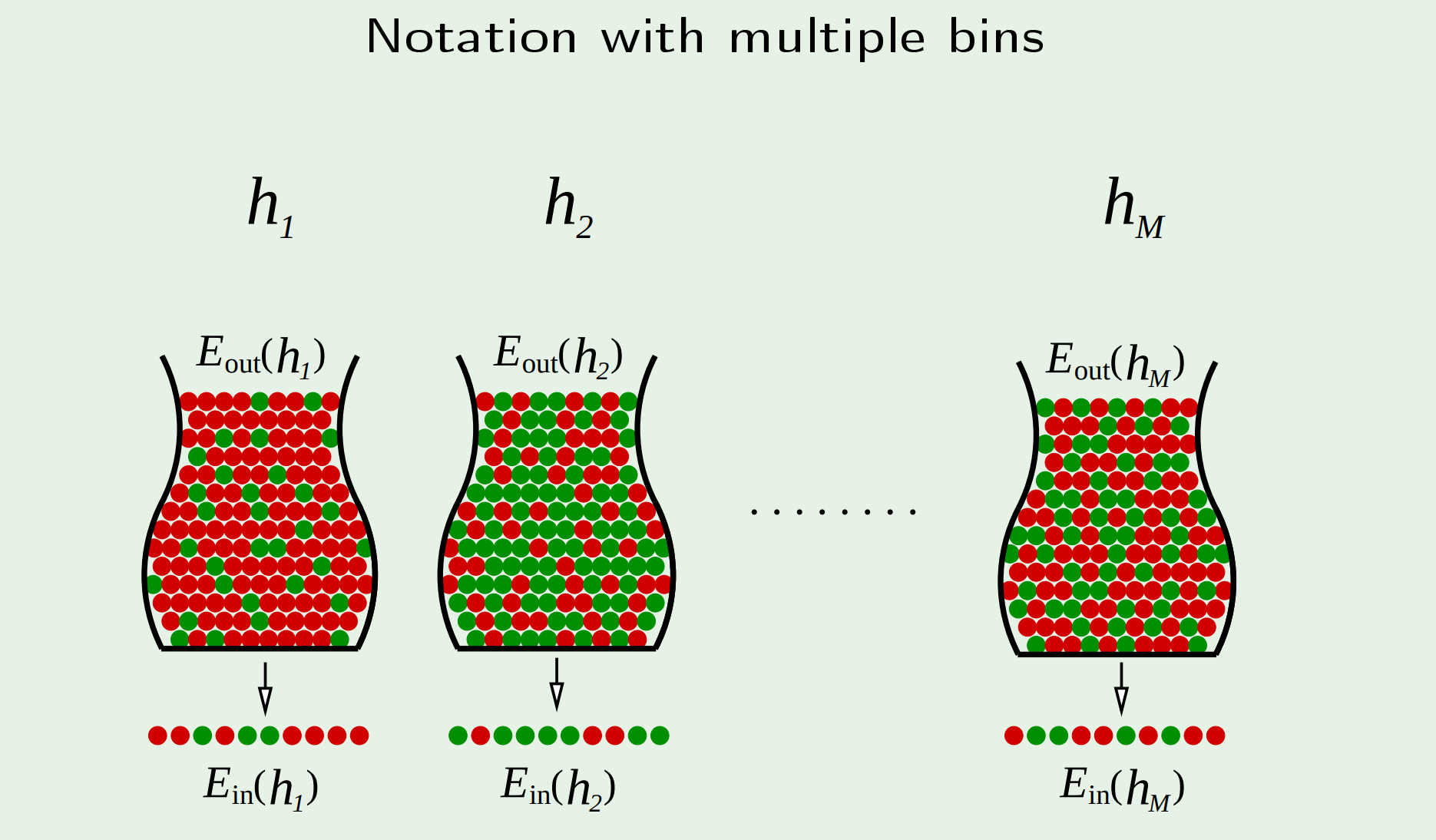
对于同一问题,使用不同的假设$h$(模型或不同参数的模型)会得到不同结果。这里的结果具体指样本内误差$E_{in}(h)$和样本外误差$E_{out}(h)$。其中一定存在一个假设$g$使得在当前的所有假设中,$g$的泛化能力最好,即$E_{in}(h)$和$E_{out}(h)$的差别最小。
所以,当你尝试一种假设并得到一组结果后,你肯定不敢相信这就是最终要寻找的那个假设——哪有那么幸运,只试了一次就找到。 所以你必然要尝试很多假设,然后从里面挑出结果最好的那个。 到这里就解释清楚为什么要引入多个模型。
但即使这样做了,我们还是要问:凭什么相信“局部最优”的假设就是你想寻找的“全局最优”假设? 这个怀疑是有道理的。 从数学上讲,在多种模型情况下的Hoeffding不等式给出的那个上界实在令人担忧。 当然这个问题会留在之后解决。
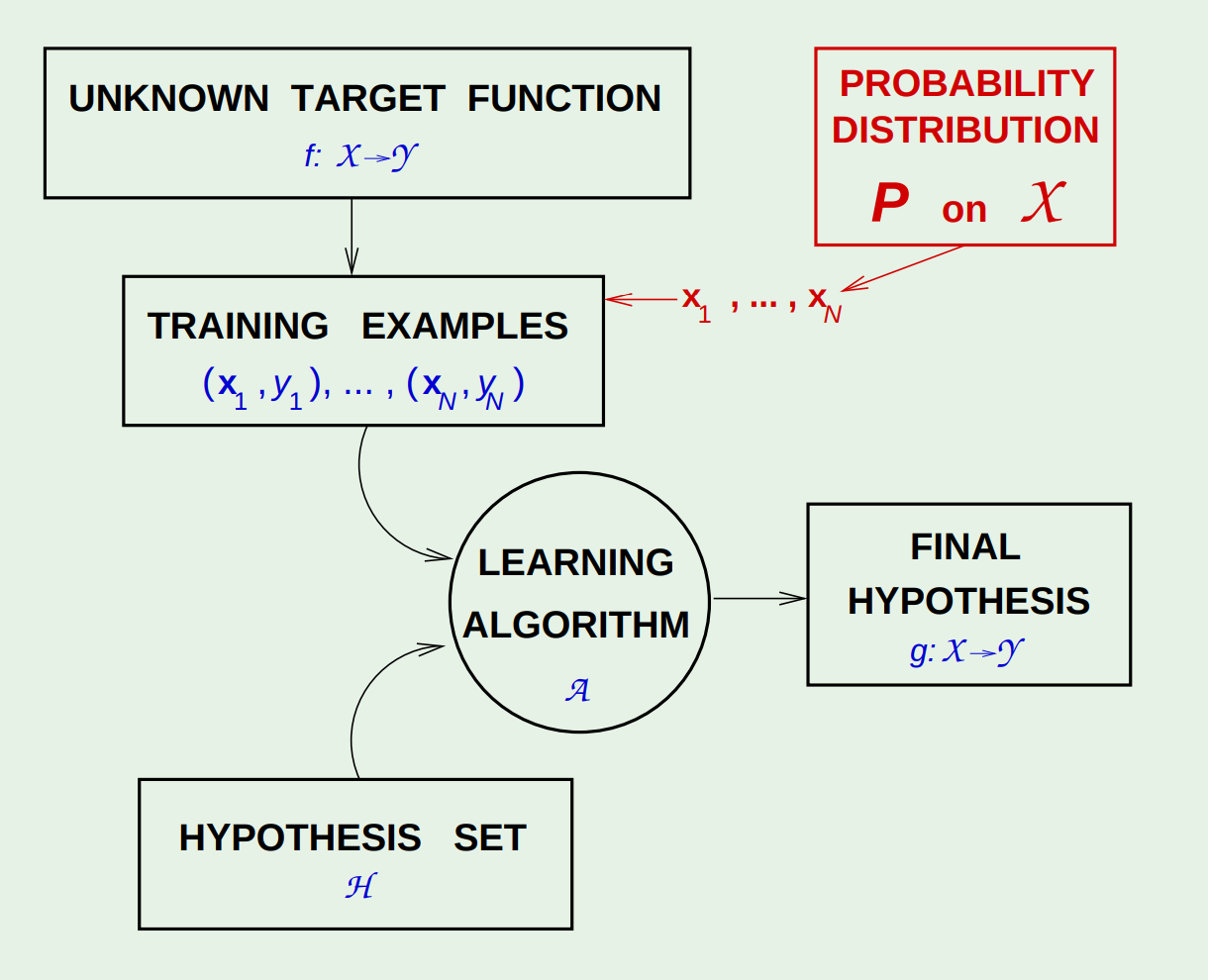
下图是教授总结的有监督学习框架。
第四课
这一讲解释了数据噪声和学习过程的关系,引出了noisy target的概念。
由于现实中的数据不可能覆盖到所有特征,因此会出现特征相同的两个实例标签却不同的情况。
也正因为此,学习的目标不再是$y=f(x)$(unknown target function),而是$P(y|x)$(target distribution),即对于给定数据$x$,有多大可能是$y$。
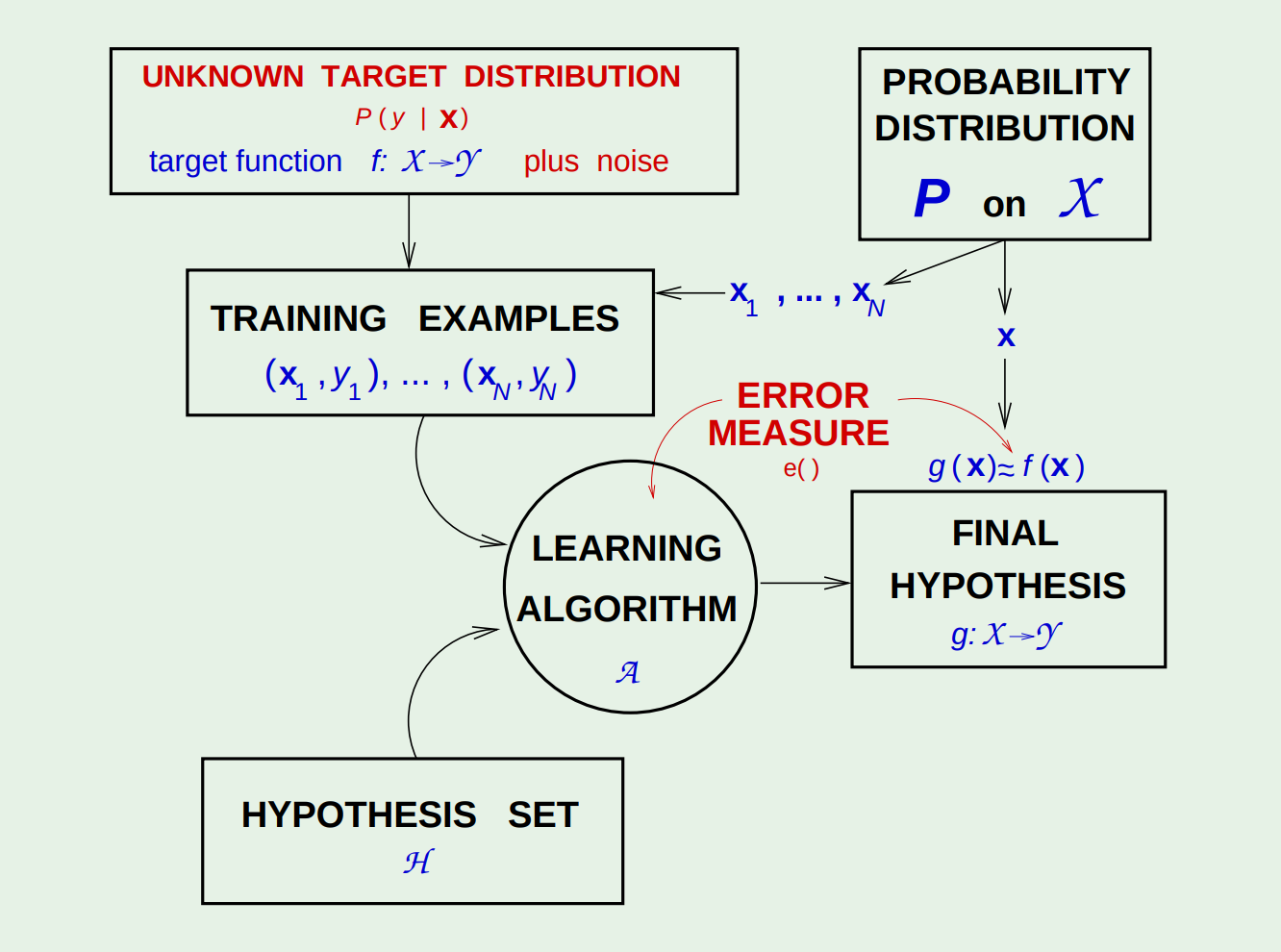
下图是新的有监督学习框架。
目前我们已经知道了,学习是可行的,即:\(E_{in}(g)\approx E_{out}(g)\)。
但这还不够,我们期望的是$g\approx f$,即:\(E_{out}(g)\approx 0\)
第五课
从考虑了多种假设的Hoeffding不等式可以看出,这个概率上界过于保守,保守的原因在于,这里的假设是这$M$个bad events之间没有重合。 所谓的bad event是指样本内误差和样本外误差超出$\epsilon$: \(\left|E_{\mathrm{in}}\left(h_{m}\right)-E_{\mathrm{out}}\left(h_{m}\right)\right|>\epsilon\)
而联合上界为:
\[\begin{aligned} \mathbb{P}\left[\mathcal{B}_{1} \text { or } \mathcal{B}_{2} \text { or } \cdots\right.&\left.\text { or } \mathcal{B}_{M}\right] \\ & \leq \underbrace{\mathbb{P}\left[\mathcal{B}_{1}\right]+\mathbb{P}\left[\mathcal{B}_{2}\right]+\cdots+\mathbb{P}\left[\mathcal{B}_{M}\right]}_{\text {no overlaps } M \text { terms }} \end{aligned}\]教授用一个例子解释了bad events之间的重合:
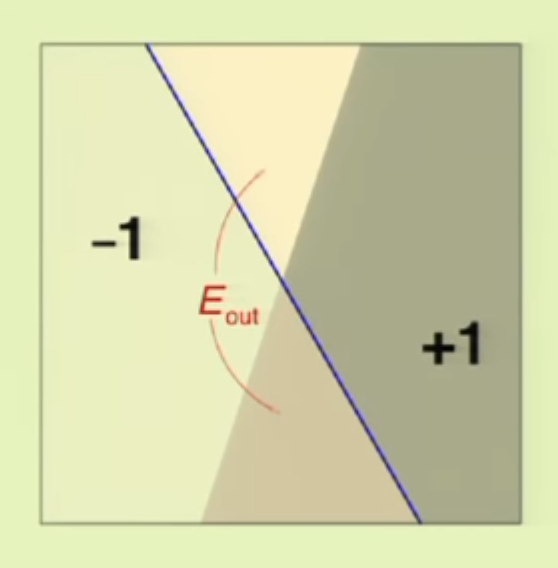
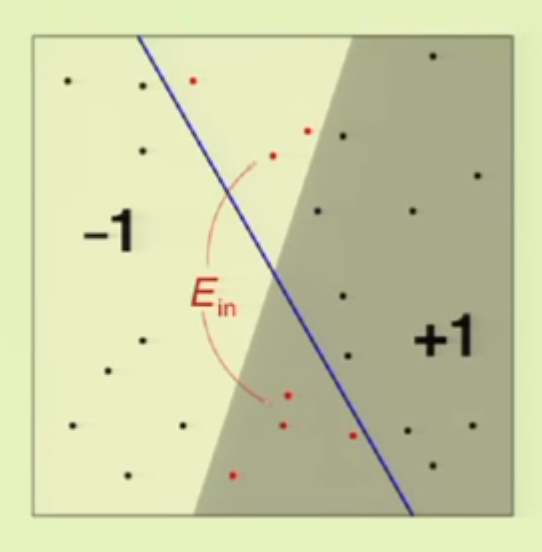
图中的蓝线代表假设,它将数据集一分为二,其中与真实数据标签不符的部分就是误差,$E_{out}$是指被误判的那部分在整个数据中所占的比例,而$E_{in}$是指采样点中被误判的那部分占所的比例。
对于另一个假设(图中绿线所示),其与第一种假设的误差明显有重合的部分(黄色部分)。
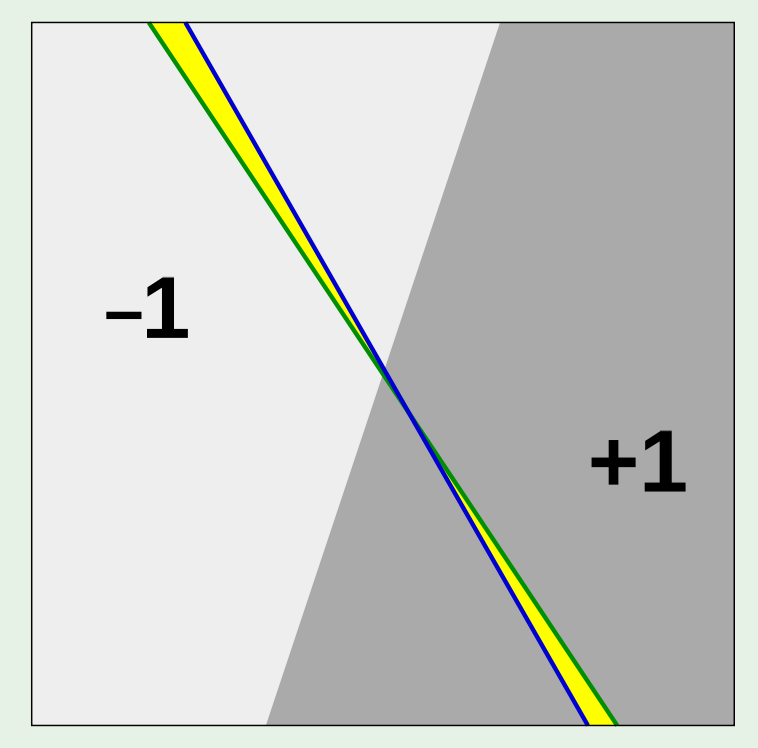
所以$M$是有机会被替换掉的。
为了替换掉$M$,这里不再考虑整个输入空间,而是只考虑有限的输入点,计算这些点的$dichotomies$。下面又是一个形象的例子:
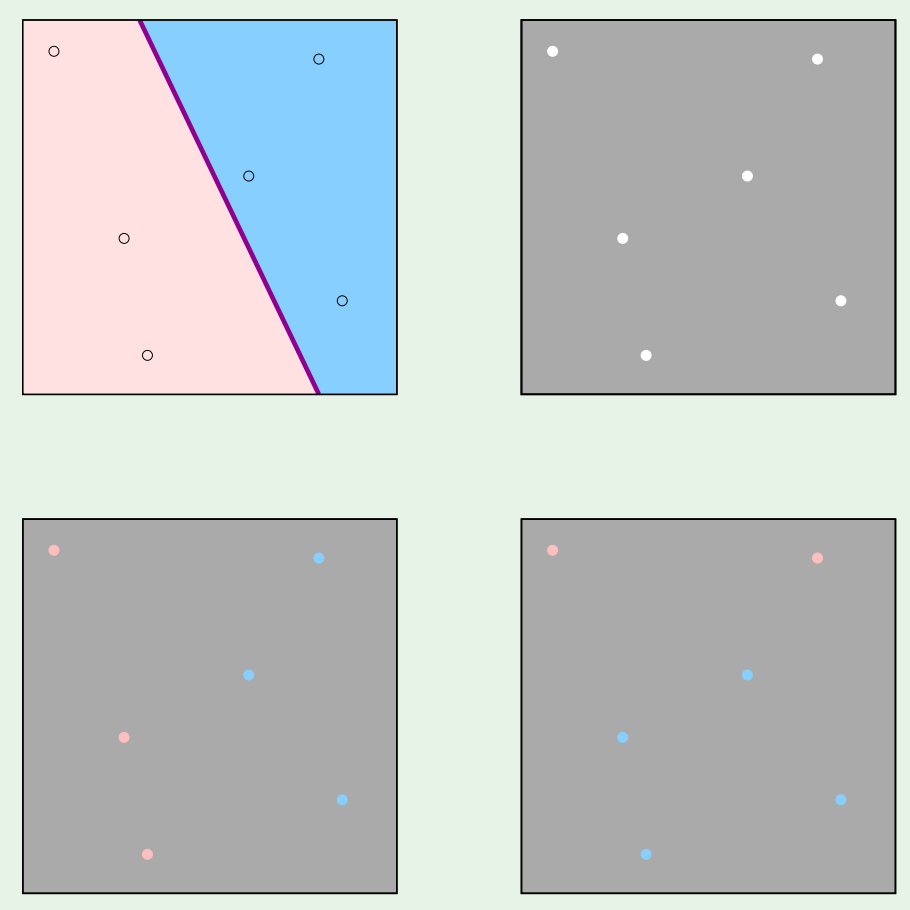
左上角的红蓝区域代表当前假设(那根直线)对输入空间的判别,但这是不可见的,因为我们无法获知整个输入空间。右上角图片可以想象成一张被打了若干个小孔的纸,叠在左上角图片上后可以透过小孔观察到小孔所属的颜色,即假设对采样点的判别。当选择不同假设时,这些采样点就会有不同的颜色。
$dichotomy$的本意是“二分”,一些点会被判定为红色,另一些点会被判定为蓝色,这样的一个划分情况被称为一个$dichotomy$。

虽然$|\mathcal{H}|$是无限的,但当无限的假设作用到有限的采样点上时,必然有很多假设会得到相同的结果,即$dichotomy$的数量有限,最多为$2^{N}$。
Growth function
生长函数的作用是,给定数量$N$,你来确定这$N$个数据点应该放在哪些位置上,使得在当前的假设集合下,得到的$dichotomy$的数量最大,并返回这个最大值。它既与假设集有关,也与数据量$N$有关。(dichotomy的数量肯定最多是$2^N$,因为存在一些划分情况是假设集无法做到的)

从无限到$2^{N}$,虽然数值依然很大,但至少是一个改进。
通过下图这一简单的例子,可以更形象地理解生长函数。
中间的小图选择的点位只能使得$dichotomy=6$,但我们对此并不关心,因为生长函数要的是最大值,即左图中的情况。
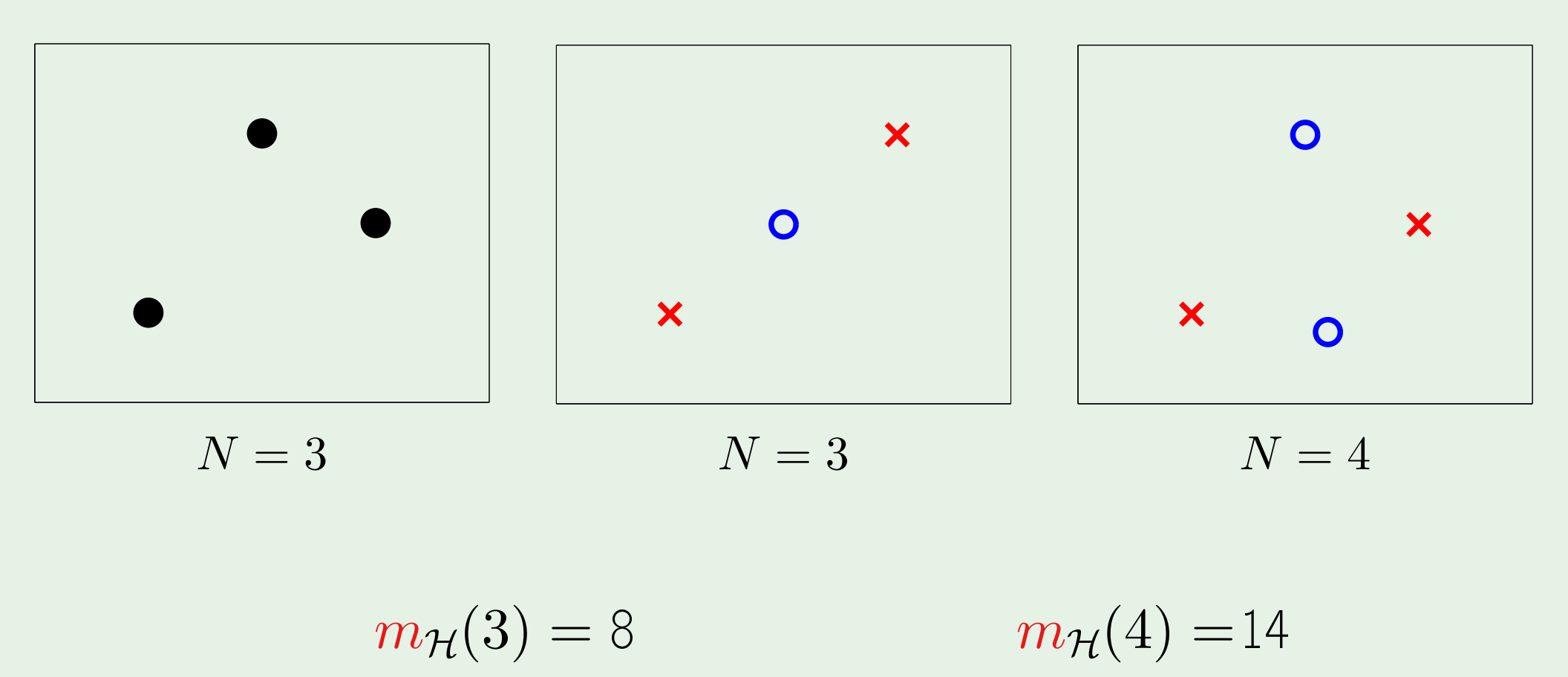
$N=4$时,数起来稍微麻烦了点,好在能数出来。但如果$N$的值更大了怎么办?
教授给出三个生长函数的实例,在这些例子中,目的都是使得$dichotomy$在当前假设集和数据量的前提下达到最大。
以第三个例子为例,任选$k$个点,在这$k$个点组成的$convex$多边形包围内的所有点都预测$+1$,否则预测$-1$。为了使得$dichotomy$最大,将$N$个数据点围成一个圈,则这N个点的任意一种排列组合都能成为一个$dichotomy$,因此$Convex Sets$的生长函数为:$m_{\mathcal{H}(N)}=2^{N}$
回到我们最初的目的,是希望找到$M$的替代。
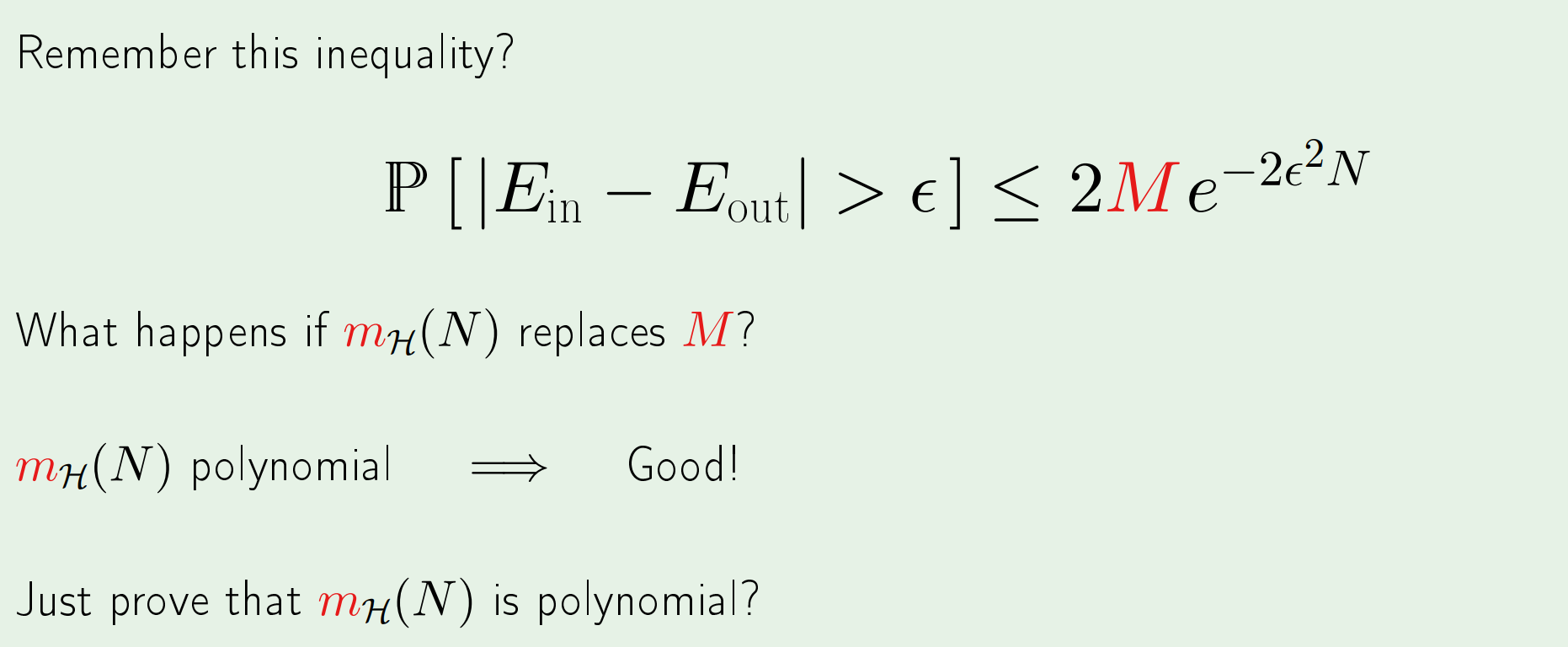
如果用生长函数来替代,由于生长函数恰好是多项式形式(polynomial),那么只要数据足够多,一定可以在概率上满足任意误差的学习。
当然,到底能不能替换要留在下节课说明。
Break point
break point是一个数值,其的直观含义是,假设集不能再将给定点“打散”(shatter,即假设集对于给定数量点的所有划分情况都可以做到)的给定点数量$k$,它表示了假设集的复杂性。\(m_{\mathcal{H}}(k)<2^{k}\)(一旦生长函数满足这一不等式,意味着假设集不能再将$k$个数据点打散,根据定义,$k$就是break point)
例如break point=3,意味着假设集无法给出三个点的所有(8种)划分情况;break point=100,意味着假设集对于$N=2\sim99$个点都可以将它们“打散”,即可以给出$2^N$种划分情况,而当点数为100时则不能。
再比如,对二维线性模型来说,它可以将3个点打散,从$m_{\mathcal{H}(3)}=8$就可以看出;而对于4个点,因为$m_{\mathcal{H}(4)}=14<2^4=16$,所以不能将4个点“打散”,即k=4是二维线性模型的break point。
上面提到过,肯定有一些划分情况是假设集无法做到的,但生长函数关心的是“最好的情况”,比如有x个点,虽然这x个点存在一种放置情况是我的假设集所不能将其分开的,但没关系,因为生长函数关心的是最大化这x个点的$dichotomy$的情况。
而break point针对的则是那些特殊情况,它关心的是当数据量到达多少时,就开始出现假设集无法将其划分的情况。
有了上述定义后,可以很方便地推出前面讲过的三个生长函数的break point。
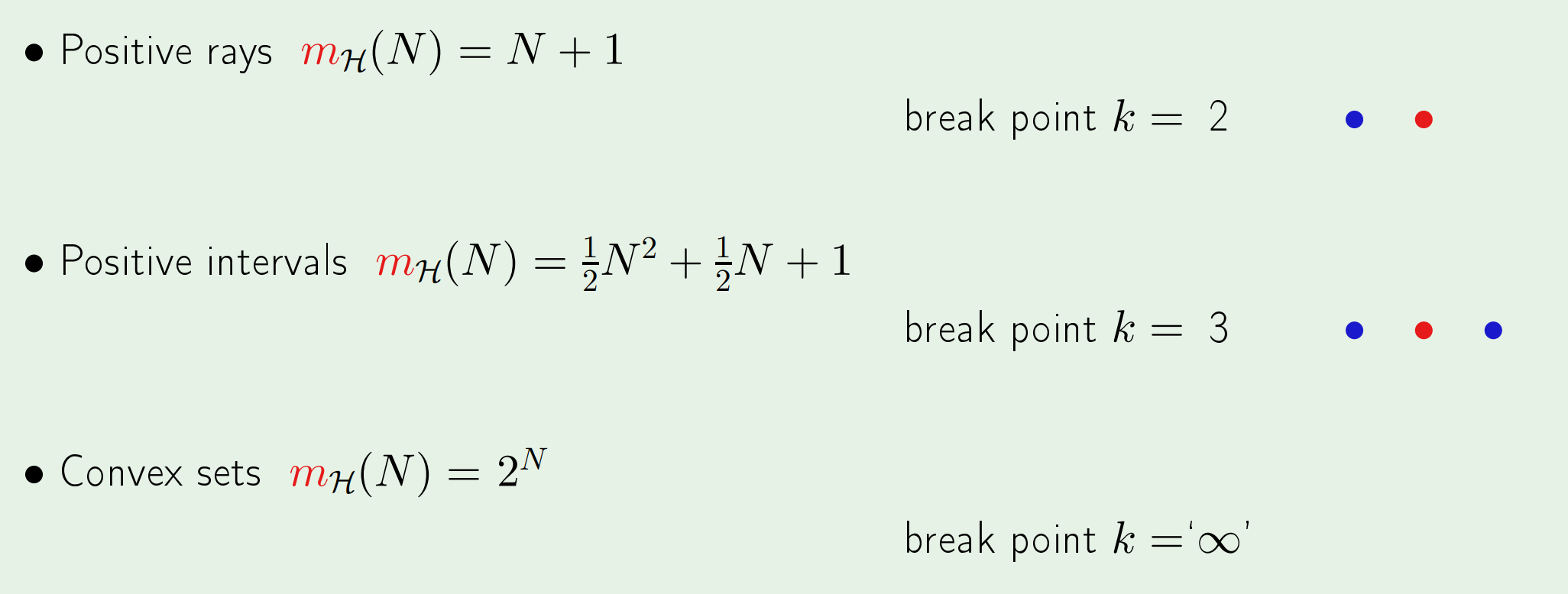
值得注意到是convex sets这个例子,对于任意数量的点,生长函数都能将其打散,所以它的break point是无穷。
进而有了以下两个结果:
\(\text { No break point } \Longrightarrow m_{\mathcal{H}}(N)=2^{N}\)(这是定义)
\(\text { Any break point } \Longrightarrow m_{\mathcal{H}}(N) \text { is polynomial in } N\)(即只要有break point,$m_{\mathcal{H}}(N)$就是N的多项式,这意味着可以学习)
小结
通过简单的分析我们知道了bad events是有重合的,于是希望寻找一个有效的量来代替$M$。生长函数描述了在给定样本量的前提下,假设集最多能给出多少种不同的划分情况,它返回的是一个有限的值。所以用生长函数来代替$M$表示在样本上的所有可能是有道理的(待证明),同时将无限变到有限。
不过生长函数的计算太难了。相比之下,计算break point看上去要简单一些。而且结论表明(待证明),只要假设集存在一个break point,那么生长函数就是样本量的多项式形式。多项式好啊,这样一来学习就成为了现实。
课后问答环节有几个有意思的问题:
1.Q:上述的理论都是针对二值函数而言,实值函数呢?
A:对于实值函数是有相应的一套理论,更technical。但我不认为有必要以及有价值去讲这些。针对二值函数的理论包含了所有你需要了解的核心思想。
2.Q:假设集能把数据点打散是件好事吗?
A:There is a tradeoff during the whole class——bad and good.如果假设集能将数据打散,说明其拟合能力强,因为你给我的数据点的任何划分我都能从假设集里找到一种假设将它们分开。 但拟合能力和泛化能力不一样,拟合能力太强的话,相应的泛化能力可能就没那么好。
3.Q:是否有系统的方法来确定break point?
A:no,通常是直接或间接估计的。
第六课
本课要解决的就是上面遗留的两个证明:
1.$m_{\mathcal{H}}(N)$是多项式;
2.$m_{\mathcal{H}}(N)$可以替换$M$;
$m_{\mathcal{H}}(N)$是多项式
为了证明$m_{\mathcal{H}}(N)$是多项式,尝试去证明$m_{\mathcal{H}}(N)\leq$一个多项式。其中用到的一个关键量是$B(N,k)$。这个量在上节课的最后出现过,其意义是对$N$个点,在break point为$k$的限制下,所能得到$dichotomies$的最大值。这里是对所有可能的假设集而言,它是生长函数关于假设集的上界。
证明的过程需要动动脑筋。先从逻辑上写出$B(N,k)$的递推关系式。
(图中的$S_2$表示那些$x_1,x_2,\ldots,x_{N-1}$的值相同,但$x_N$的值既有$-1$也有$+1$的$dichotomy$;$S_1$与之相反)
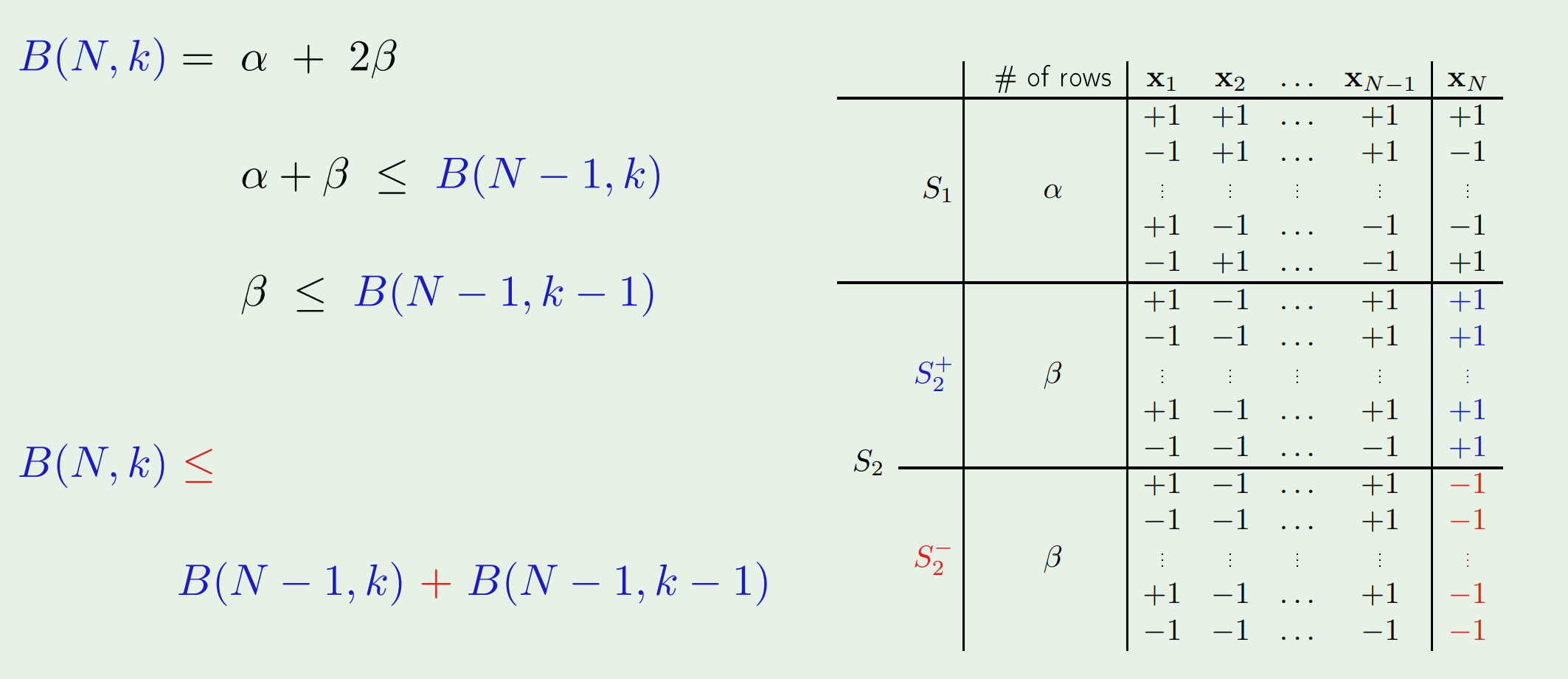
然后既可以从图中归纳出$B(N,k)$的上界,也可以进一步得到$B(N,k)$上界的解析表达式。
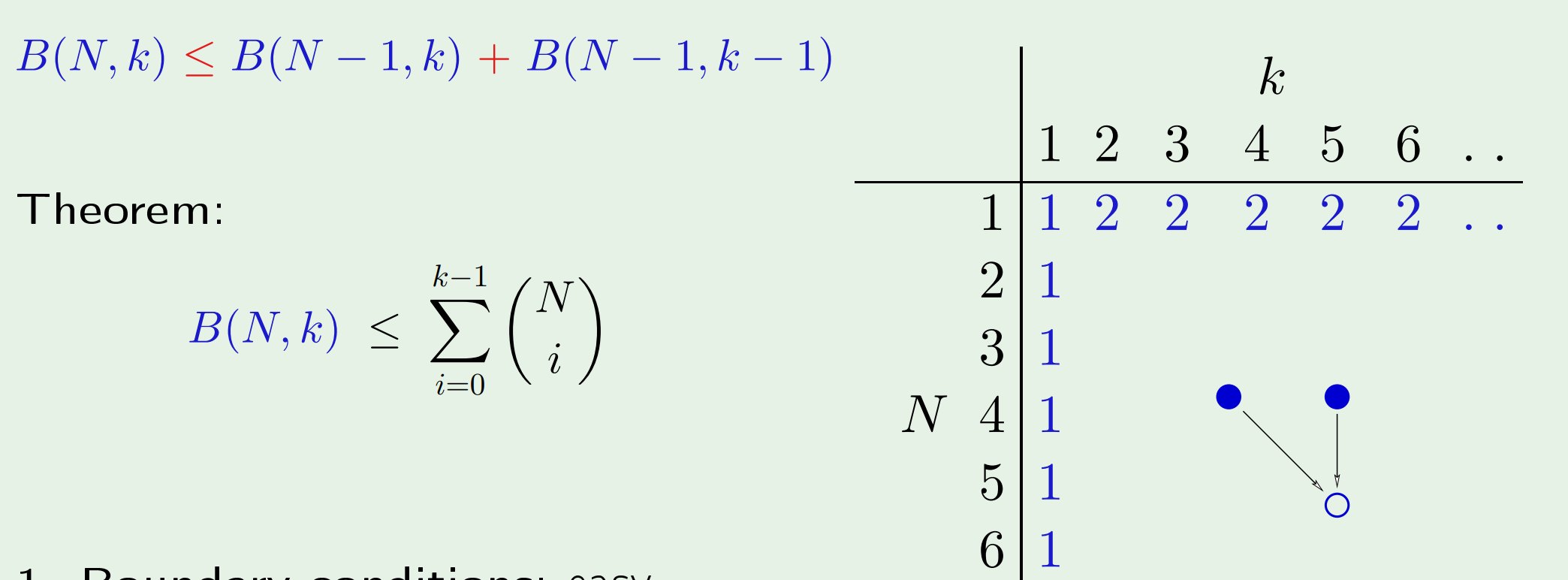
最终有如下结论:
给定假设集$\mathcal{H}$,其break point $\mathcal{k}$也随之确定,\(m_{\mathcal{H}}(N) \leq B(N,k) \leq\underbrace{\sum_{i=0}^{k-1}\left(\begin{array}{c}{N} \\ {i}\end{array}\right)}_{\text {maximum power is } N^{k-1}}\) 因为k是一个常数,所以$N^{k-1}$是多项式。
$m_{\mathcal{H}}(N)$可以替换$M$
教授说严谨的证明有6页之多,但有必要解释清楚其中的一些关键,以便于理解详细的证明。
需要解释清楚三件事:
一是,我们知道$M$是假设没有重合,但生长函数是怎么和重合扯上关系的呢?
二是,生长函数针对的是$E_{in}$,但和整个空间联系的是$E_{out}$。
三是,把上述两点组合起来得到结论。
通过这张图可以形象地理解:
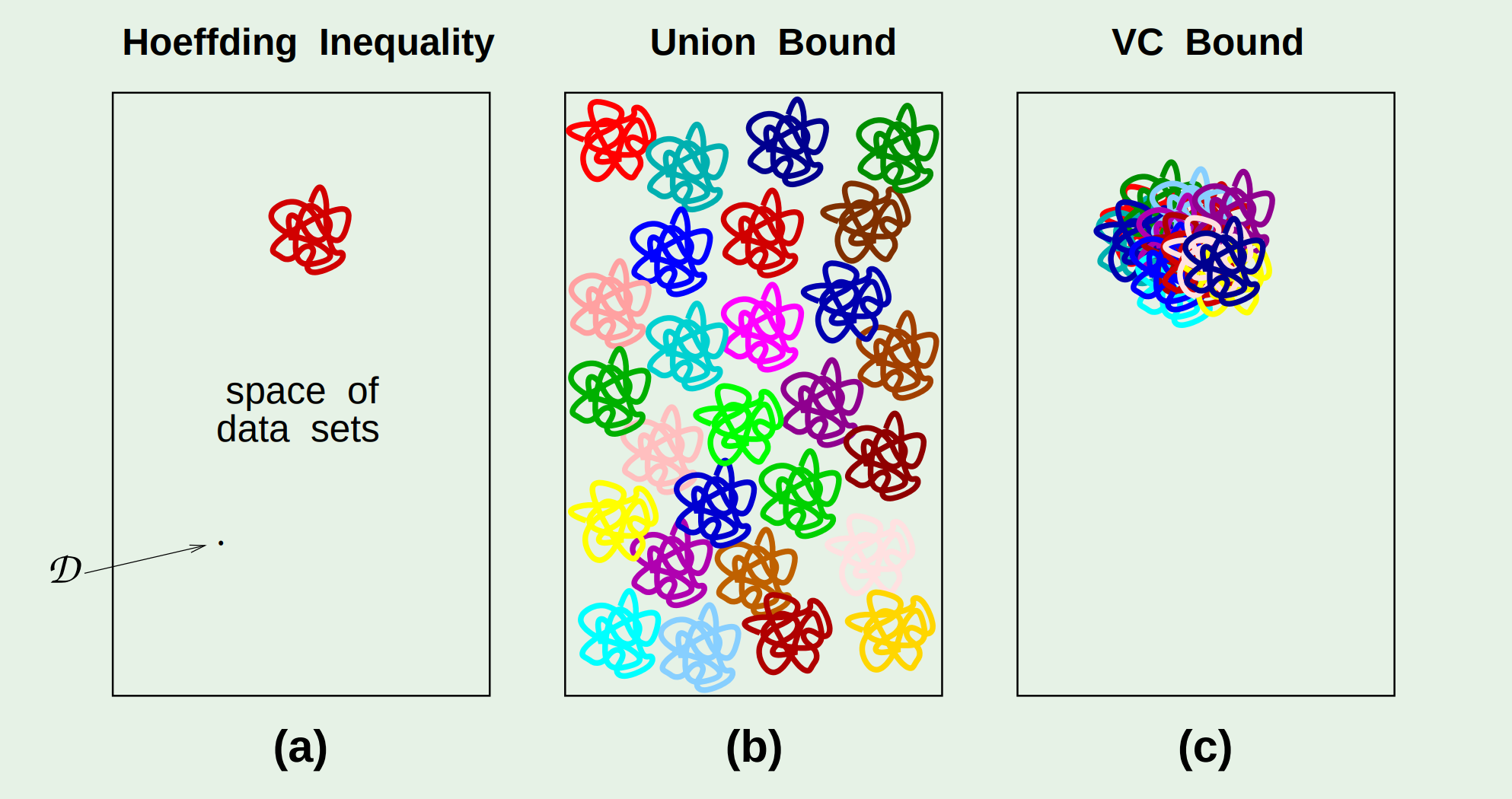
图(a)的长方形表示整个数据空间,其中的点表示采样数据($x_1,x_2,\cdots,x_N$)。如果当前假设在这个点上表现为bad event,则被涂成红色。由Hoeffding不等式保证bad events的区域(图(a)中的红色区域)较小。
图(b)不同颜色的区域代表的是使不同的假设出现bad events的采样数据。这是无重合的情况,即$M$。可以发现很快就能填满整个数据空间。
图(c)是在VC bound下的bad events的区域。
教授对图(c)进一步给出了说明:假设一个被涂了颜色的点一共会被涂上100种不同的颜色,即有100个假设会在这组采样数据上出现bad event。那么它可想而知,整个bad events的区域会缩减为原来的1%。
很多不同的假设会给出相同的$dichotomy$,即这些假设在有限数据点上的表现一致(对数据点的分类结果一致)!所以一旦有一个假设在这组数据点上表现出bad event,那么和它表现一致的那些假设都在该组数据点上表现为bad events。而生长函数正好就是反映了$dichotomy$的这种冗余,从而体现出了生长函数和重合的关系。
关于如何过渡到$E_{out}$,只有一页slide,只是启发性的告诉了通过$\left|E_{i n}-E_{i n}^{\prime}\right|$来解决$\left|E_{i n}-E_{o u t}\right|$ 具体来说,Hoeffding之所以会变得如此松弛,是因为我们使用了多个假设(不同的假设对应着不同的罐子),并给出最差的那个需要满足的上界。现在换一个思路,如果只从一个罐子中两次采样,我们有理由相信这两次采样数据之间的经验误差是有联系的(比如我们对3000人做民调,再对另外不同的3000人做民调,我们有理由相信两次结果在很大概率上相近),这种联系很像只做一次采样的经验误差和泛化误差的那种联系。 但是需要知道的是,一旦我们换成这种多次采样的思路,那么数据就从整个数据空间变到了有限点集上,而有限点集就能用$dichotomy$来处理。 这是阅读详细证明需要知道的一点。
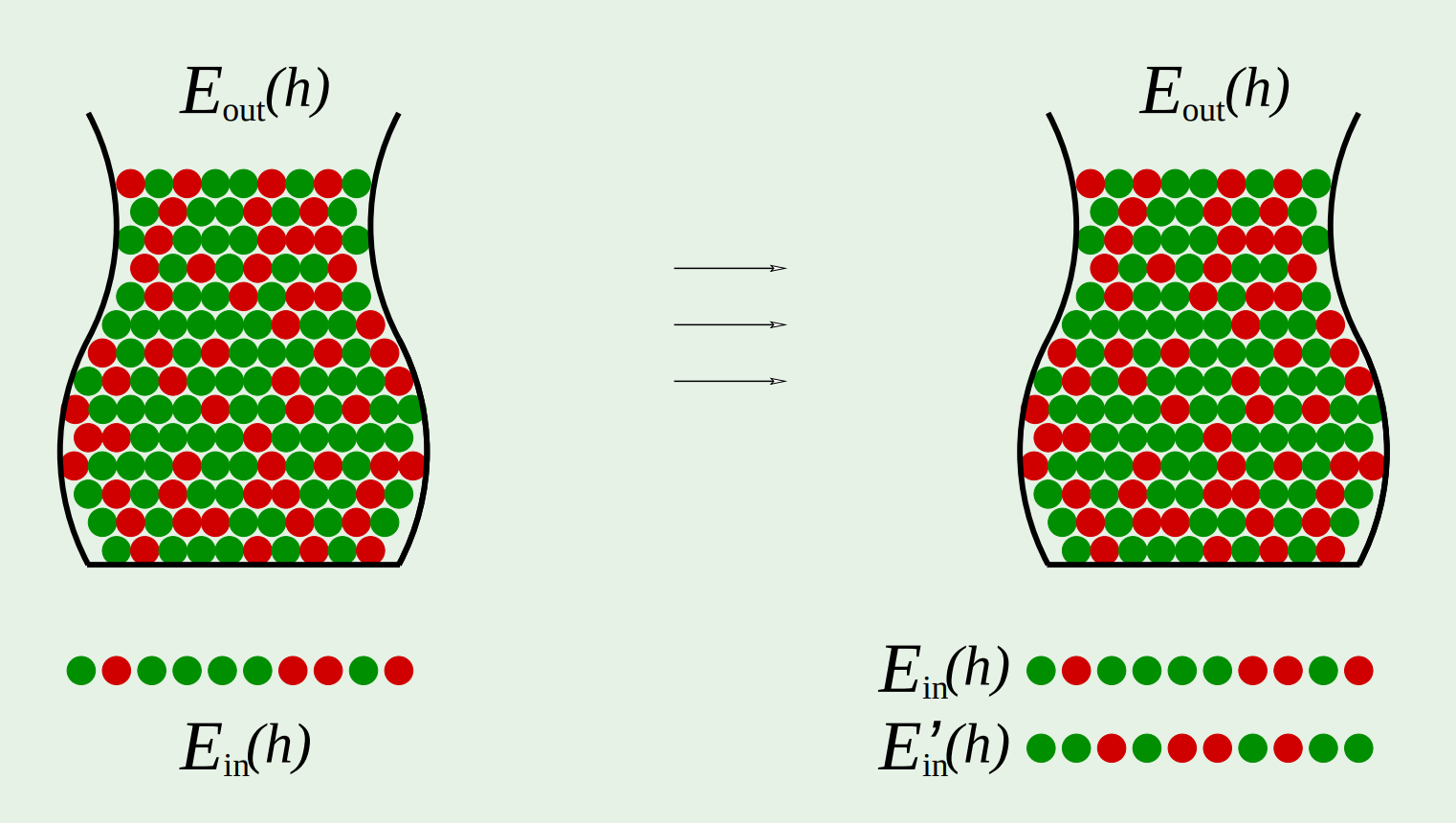
最后是将两点组合到一起:
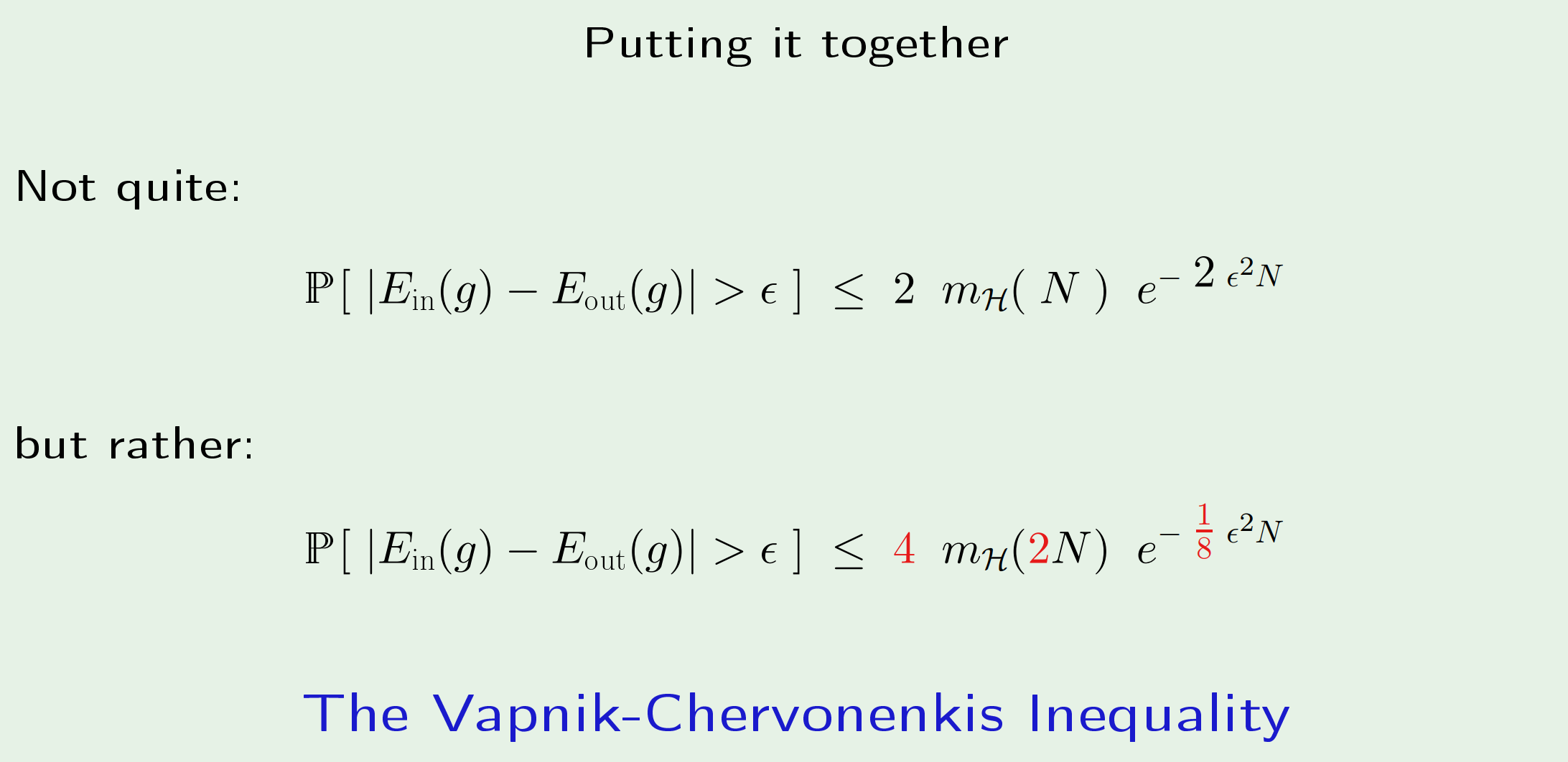
图中的第一个公式是“not quite”的,因为用$m_{\mathcal{H}}(N)$替换$M$的想法是没问题的,但具体换的时候要对细节的地方做修改,于是就有了第二个式子。
第七课:VC维
给定一个假设集$\mathcal{H}$,它的VC维记作$d_{\mathrm{VC}}(\mathcal{H})$,表示$\mathcal{H}$最多能打散的点的数量。
数值上等于$break point-1$(假设这个数量为n,不是说对所有n个点的数据集都能打散,而是至少有一组数据集能够打散),教授解释VC维和break point的区别仅在于一个是从正面描述最多能打散的数量,另一个是从反面描述达到多少之后就不能打散了。
然后证明了感知机的VC维等于其参数的个数,并解释对于感知机而言,参数的个数可以代表自由度,并举了一个特例来说明VC维的数量度量的是有效参数的个数。
对于较复杂的模型来说,确定VC维是件困难的事情,但可以通过模型的自由度来近似得到VC维的上界。这也就是为什么对神经网络而言,通常取$d(\mathrm{VC})=O(\mathrm{VD})$。
回到VC不等式来研究样本数量$N$随$d_{\mathrm{VC}}$的变化。
经验结论是$N \geq 10 d_{\mathrm{VC}}$才能保证可学习。 此外,VC维是生长函数密切相关,可以用来计算生长函数的上界: 定理:若假设空间$\mathcal{H}$的VC维为$d$,则对于任意整数$N\geq d$有: \(m_{\mathcal{H}}(N)\leq \left(\frac{eN}{d}\right)^d\)
最后给出了泛化界: