多任务学习概述

多任务学习（MTL，multi-task learning）最早可以追溯到1997年的一篇文章，它描述的是一种学习范式——多个任务的数据一起来学习，学习的效果有可能要比每个任务单独学习的结果要好。本质上是利用多个任务的共享信息来提高在所有任务上的泛化性。

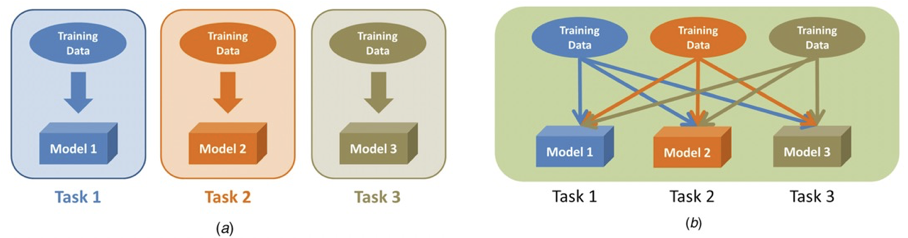
好处是：

1. 一次性学习多个任务：效率高，部署时占用内存小；
2. （可能）比每个任务单独学习的效果更好：共享互补信息、彼此正则化，提高泛化性

接下来给出形式化定义。了解定义可以帮助我们理清前人的工作都是从哪些方面做出了改进。

定义

\[\min_{\substack{\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{1}, \ldots, \boldsymbol{\theta}^{T}}} \sum_{t=1}^{T} c^{t} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)\]

其中，$c^t$是第$t$个任务的权重，$\theta^{sh}$和$\theta^{t}$分别是模型中多个任务的共享参数和各自独享的参数，$\hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)$是第$t$个任务的经验损失：\(\hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right) \triangleq \frac{1}{N} \sum_{i} \mathcal{L}\left(f^{t}\left(\mathbf{x}_{i} ; \boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right), y_{i}^{t}\right)\)。

现在我们来审视这个定义，会发现定义中主要有两部分存在较大的操作空间。第一部分是权重$c^t$，即每个任务的重要程度；第二部分是模型参数$\theta^{sh}$和$\theta^t$，即共享哪些参数、共享多少。按照这两种角度，本文会将过去的一些研究工作分成这两类，以提供一种了解MTL的视角。

平衡损失

这类方法的核心就是给每个任务找到一个合适的权重，目标是使整体损失降到最低，同时优化的结果还要在各个任务上都比单独学习要好。

首先，为什么要平衡不同的损失，或者反过来想，不平衡行不行？答案是不行，有两个原因：

1. 不同任务的重要性不同，我们更希望模型能优先在那些重要的任务表现更好；
2. 不同任务的优化难度不同，如果不调整权重，所有任务平等看待，那些难以优化的任务可能在一次学习过程中欠拟合。

综上，我们需要去调整权重来使各个任务都得到较好的学习。

在引入研究工作之前，我们不妨自己先想一想，从设置权重的角度该怎么做MTL。

最朴素的想法就是按照任务的重要程度，先验地给不同任务分配一个权重。比如有两个任务$t_1$和$t_2$，其中$t_2$比较重要，那么就可以给$t_2$的损失函数乘以2。从反向传播来看，更新的梯度也会相应的乘以该系数，从而在参数更新中占到更大的比重。

这里需要补充一个误区。就是不能通过损失值的大小来判断任务的重要程度。比如有个任务的loss值很大，这时候就很容易慌乱，觉得是不是对这个任务的优化力度不够，于是本能地调大这个任务的权重，期望将这个任务的loss降下来。这样做是不合理的。首先，正常场景下的学习任务都不会把loss将至0，优化的结果一般是loss会稳定在某一区间内。这既取决于任务本身的学习难度（loss就是没法再降下去），也取决于输出值的量纲（比如预测结果的单位）。

\[loss = l_1 + 2*l_2 \\ grad = \frac{\partial l_1}{\partial \theta} + 2*\frac{\partial l_2}{\partial \theta} \\ \hat{\theta} = \theta + \lambda \ grad\]

太简单的做法一般都有问题，这种做的问题是：

1. 先验权重不是最优：乘的系数只是一厢情愿；比如如果$l_1$本身的梯度就很大，那么即使给$l_2$增加权重也是杯水车薪；
2. 权重固定：不同任务的梯度的相对大小会在优化过程中发生改变，显然一套固定的权重不可能应对整个优化过程；

接下来要介绍的两篇文章就是针对上述问题给出了各自的解决办法。

Uncertainty Weighting——不确定性加权¹

这篇文章的核心是动态调整不同任务的权重，换言之就是去学习权重。我认为直接看公式即可，前面的理论部分比较虚，像是先有了trick再去补充动机。感兴趣的可以去读它的原文。

它首先假设每个任务的真值的后验分布是以预测值为均值的正态分布，方差是噪声，表示了任务的难易程度：

\[p\left(\mathbf{y} \mid \mathbf{f}^{\mathbf{W}}(\mathbf{x})\right)=\mathcal{N}\left(\mathbf{f}^{\mathbf{W}}(\mathbf{x}), \sigma^{2}\right)\]

简单来说就是，真值大概率就在预测值的附近。

以两个任务为例，联合分布为：

\[\begin{aligned} p\left(\mathbf{y}_{1}, \mathbf{y}_{2} \mid \mathbf{f}^{\mathbf{W}}(\mathbf{x})\right) &=p\left(\mathbf{y}_{1} \mid \mathbf{f}^{\mathbf{W}}(\mathbf{x})\right) \cdot p\left(\mathbf{y}_{2} \mid \mathbf{f}^{\mathbf{W}}(\mathbf{x})\right) \\ &=\mathcal{N}\left(\mathbf{y}_{1} ; \mathbf{f}^{\mathbf{W}}(\mathbf{x}), \sigma_{1}^{2}\right) \cdot \mathcal{N}\left(\mathbf{y}_{2} ; \mathbf{f}^{\mathbf{W}}(\mathbf{x}), \sigma_{2}^{2}\right) \end{aligned}\]

优化目标就变成了求这个概率的最大似然，等价于去最小化它的相反数：

\[\begin{aligned} &=-\log p\left(\mathbf{y}_{1}, \mathbf{y}_{2} \mid \mathbf{f}^{\mathbf{W}}(\mathbf{x})\right) \\ &\propto \frac{1}{2 \sigma_{1}^{2}}\left\|\mathbf{y}_{1}-\mathbf{f}^{\mathbf{W}}(\mathbf{x})\right\|^{2}+\frac{1}{2 \sigma_{2}^{2}}\left\|\mathbf{y}_{2}-\mathbf{f}^{\mathbf{W}}(\mathbf{x})\right\|^{2}+\log \sigma_{1} \sigma_{2} \\ &=\frac{1}{2 \sigma_{1}^{2}} \mathcal{L}_{1}(\mathbf{W})+\frac{1}{2 \sigma_{2}^{2}} \mathcal{L}_{2}(\mathbf{W})+\log \sigma_{1} \sigma_{2} \end{aligned}\]

本文的核心就是这个公式。如果直接预测权重的话，会很快使权重收敛到0（因为这样损失值就是0了）。文章提出的这个公式相当于给权重加了一个正则化项，防止权重为0。它的另一个好处是，对于那些难以优化的任务（即任务的不确定性更大、噪声大），可以学习到一个较小的权重；相应的，对于简单的任务，会学到一个较大的权重，从而使模型关注那些简单的任务。

Gradient Normalization——梯度标准化²

这篇文章的目的是使不同任务以相近的速度来学习，具体是通过每次反向传播前调整每个任务的梯度来实现的。简单来说，每一步迭代会将每个任务的当前loss与各自的上一步迭代的loss求比值，比值越大，说明该任务的越难优化。据此可以量化每个任务的优化难度。那么在反向传播时，就会给优化难度大的任务的梯度值乘以一个较大的权重，以增大其影响；相应的，对优化难度较小的任务的梯度值乘以一个较小的权重，减弱其对参数更新的影响。

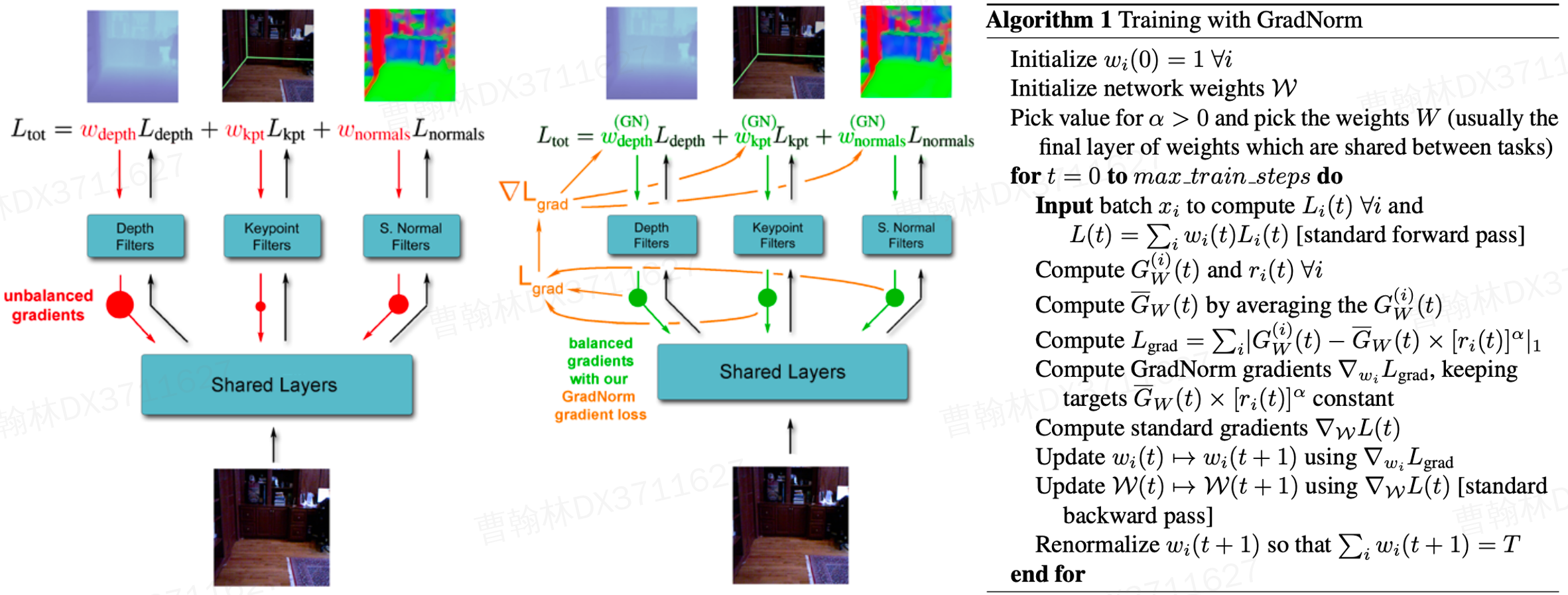
具体实现时，是在网络的最后加一层权重参数。首先，每次前向传播时就算出每个任务的loss，通过上述的loss比值计算出各任务调整后的梯度；然后，根据当前梯度和调整后梯度的差值，优化最后一层的权重参数，目的是将权重参数调整至各任务梯度相近的效果；最后固定住权重层的参数，做正常的反向传播，优化其余网络参数。

Multi-Objective Optimization——多目标优化³

这篇文章把MTL看做是多目标优化问题。在作者看来，给目标乘以或静态或动态的权重，其实是将多目标优化问题变成了优化加权后的单目标优化问题。但这种调权重的方法的问题是，如果多个任务间存在竞争的关系——一个任务变好，其它另任务就会变差，那么就很难找到一组有效的权重了。而作者采用的方法是将MTL看做一个带约束优化问题，求解它的过程就是寻找帕累托最优的过程，即如果一个任务的变好，是在其他任务变差的前提下实现，那么我们就称达到帕累托最优。形象地讲，在刚开始优化时，每个任务都能变好，直到优化到某一步，发现一个任务变好但至少有一个其他任务会变差，那么我们就认为达到了帕累托最优，优化结束。

将MTL形式化：

\[\min _{\substack{\boldsymbol{\theta}^{sh} \\ \boldsymbol{\theta}^{1}, \ldots, \boldsymbol{\theta}^{T}}} \mathbf{L}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{1}, \ldots, \boldsymbol{\theta}^{T}\right)=\min _{\substack{\boldsymbol{\theta}^{sh} \\ \boldsymbol{\theta}^{1}, \ldots, \boldsymbol{\theta}^{T}}}\left(\hat{\mathcal{L}}^{1}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{1}\right), \ldots, \hat{\mathcal{L}}^{T}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{T}\right)\right)^{\top}\]

要求解这个问题，等价于求解一个等式约束优化问题。

根据multiple gradient descent algorithm (MGDA) （一篇优化方向的数学论文），我们知道了可以通过其KKT条件来寻找满足帕累托最优的驻点。

1. \(∃ \alpha^{1}, \ldots, \alpha^{T} \geq 0 \ s.t. \ \sum_{t=1}^{T}\alpha^t=1\)且 \(\sum_{t=1}^{T} \alpha^{t} \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)=0\)
2. $\forall t, \nabla_{\boldsymbol{\theta}^{t}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)=0$

接下来我将这篇文章的方法拆解为四部分来解释。

问题变换

先看上面的第二个条件，很简单，就是让每个任务独享的那部分参数梯度为零，只要通过标准的梯度下降法优化就行，运气好的话总能满足该条件。OK，求解$\theta^{t}$搞定。

然后再看第一个条件，好像一下子不知道该怎么求解$\theta^{sh}$。好在MGDA证明了，通过求解下列优化问题，要么直接找到满足KKT条件的解$\theta^{sh}$，即最小值为0；要么沿着$\sum_{t=1}^{T}\alpha^t \nabla_{\theta^{sh}}$更新能使所有任务都有所改进：

\[\min _{\alpha^{1}, \ldots, \alpha^{T}}\left\{\left\|\sum_{t=1}^{T} \alpha^{t} \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)\right\|_{2}^{2} \mid \sum_{t=1}^{T} \alpha^{t}=1, \alpha^{t} \geq 0 \quad \forall t\right\}\]

求解新问题

于是求解MTL问题只剩下求解上述优化问题。而这个问题，本质上就是在一个凸包里找一个点，使得距离已知点最近。这是在优化方向被广泛研究的问题。Frank-Wolfe算法就是求解这类带约束的凸优化问题的一种算法。

更新MTL参数

到此我们就知道该怎么求解$\theta^{sh}$和$\theta^{t}$了，接下来就是更新网络参数：

改进：优化上界

上述算法虽然可以求解问题，但效率太低。直观表现就是每个任务都要计算针对共享参数的梯度，反向传播的计算量就和任务的数量成正比；当共享参数量很大时，非常低效。其实直到这里才引入了这篇文章的主要工作（之前的算法都是前人的成果，不过作者在本文对这些方法做了更易懂的解释，也是一大贡献）。对于encoder-decoder的网络，作者以encoder的结果为界，将反向传播的链条分成两部分：

\[f^ {t}(x;\theta^{sh},\theta^{t})=(f^{t} (\cdot ;\theta ^ {t})^ \circ g(\cdot; \theta ^{sh}))(x)= f^ {t} (g(x; \theta ^ {sh} ); \theta ^ {t} )\] \[f^{t}\left(\mathbf{x} ; \boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)=\left(f^{t}\left(\cdot ; \boldsymbol{\theta}^{t}\right) \circ g\left(\cdot ; \boldsymbol{\theta}^{s h}\right)\right)(\mathbf{x})=f^{t}\left(g\left(\mathbf{x} ; \boldsymbol{\theta}^{s h}\right) ; \boldsymbol{\theta}^{t}\right)\]

将压缩层的表征向量记为$Z$ ，易得原优化目标的上界：

\[\left\|\sum_{t=1}^{T} \alpha^{t} \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)\right\|_{2}^{2} \leq\left\|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right\|_{2}^{2}\left\|\sum_{t=1}^{T} \alpha^{t} \nabla_{\mathbf{Z}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)\right\|_{2}^{2}\]

这样做的好处是，反向传播时每个任务的只需要计算对$Z$的梯度即可，$Z$的量级相比$\theta^{sh}$小很多，因此计算量会大大减小。由于$\left|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right|_{2}^{2}$与我们要计算的$\alpha$无关，因此可以去掉。用该上界替换原优化目标，优化问题就近似成：

\[\min _{\alpha^{1}, \ldots, \alpha^{T}}\left\{\left\|\sum_{t=1}^{T} \alpha^{t} \nabla_{\mathbf{Z}} \hat{\mathcal{L}}^{t}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^{t}\right)\right\|_{2}^{2} \mid \sum_{t=1}^{T} \alpha^{t}=1, \alpha^{t} \geq 0 \quad \forall t\right\}\]

文章证明了这种近似依然能达到帕累托最优。

设计网络结构

从网络结构上来看，上述三种方法都是基于 Share-Bottom 网络结构，底层参数共享，上层分别用不同的网络学习不同的任务，然后从优化的角度提升在所有任务上的表现。而设计网络结构的方法就是大力出奇迹了，它不关心每个任务学得怎么样，先验地设计好网络结构后，剩下就交给模型自己去学了。这类方法看谷歌的MMOE这一篇就够了，其余的万变不离其宗。

MMOE⁴

MMOE想解决的问题是同样是任务间存在竞争关系情况下的MTL。它将底层参数分解成多个专家网络、并利用门控机制为每个任务找到合适的输入向量。其中门控机制的作用是计算出一组权重，来对底层各部分输出的向量进行加权，并作为上层任务的输入。一图胜千言：

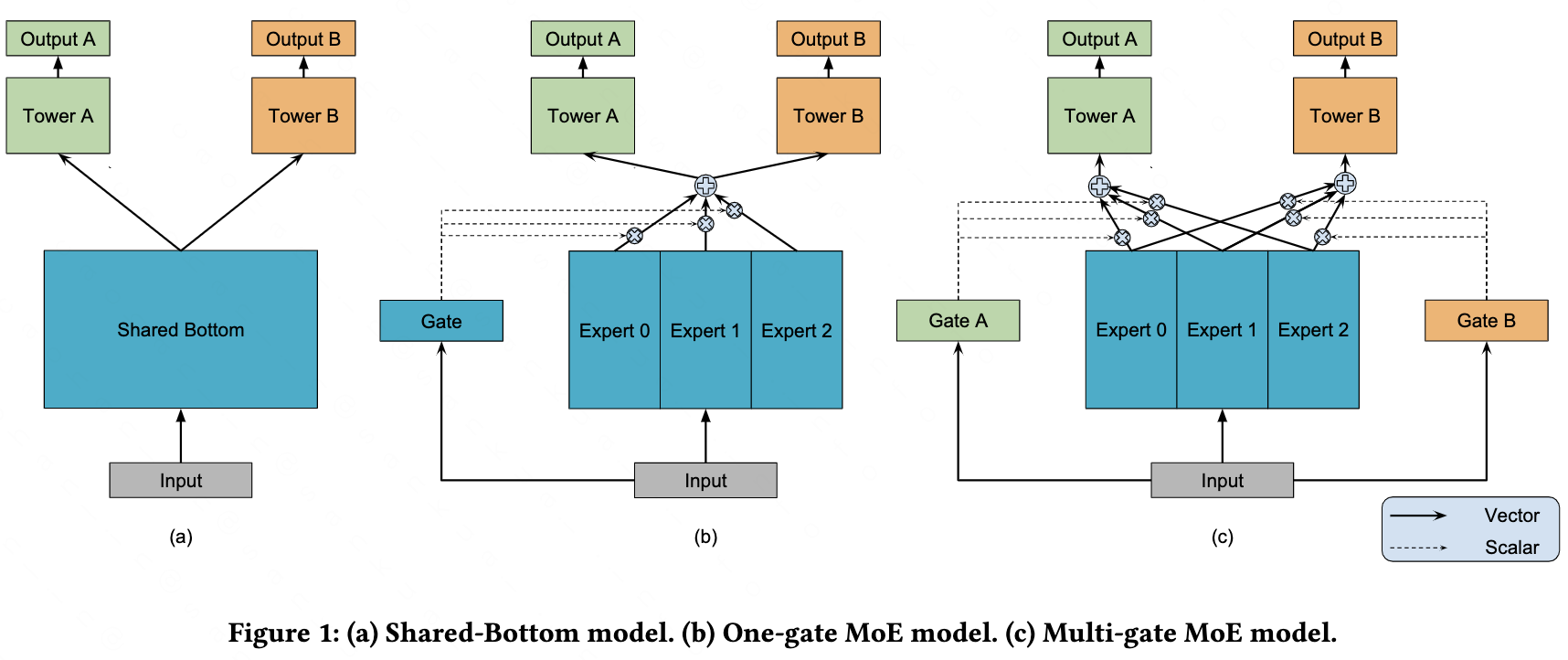
小结

把MMOE和损失平衡的方法放在一起看，其实它们在本质上都是在学习动态权重。只不过损失平衡的方法是将权重加在最后的损失函数上，为了避免权重退化成0，因此加了正则化或是两步优化；MMOE则是把权重放在了模型内部，暴力学习，省事，就是权重不太直观。

参考文献：