本章通过实例对线性模型的稳健性优化进行了分析。线性模型虽然特殊且简单,但却可以给我们带来一些直观的启发。
Chapter 2:线性模型
在谈论针对深度神经网络的对抗和攻击之前有必要先看看假设函数是线性的情况,即对一个多分类的情况\(h_\theta : \mathbb{R}^n \rightarrow \mathbb{R}^k\),我们假设分类器的形式是:
\[h_\theta(x) = W x + b\]其中\(\theta = \{W \in \mathbb{R}^{k \times n}, b \in \mathbb{R}^k\}\)。首先以最简单的二分类问题为例进行说明,因为许多概念在二分类的情况下会更容易描述。然后将这个假设函数代入到我们之前的稳健性优化框架:
\[\DeclareMathOperator*{\minimize}{minimize} \minimize_{W,b} \frac{1}{|D|} \sum_{x,y \in D} \max_{\|\delta\| \leq \epsilon}\ell(W(x+\delta) + b, y).\]需要强调的是,在上述形式下,我们恰好可以求解出内部优化问题的紧致上界,并给多分类情况提供一个较紧的上界。而且外部的最小化问题也是凸的,所以进而可以求解出全局的最优解(二分类情况)。与之形成鲜明对比的是,对于深度神经网络而言,由于神经网络本身是非凸的,因此不管是最小化还是最大化问题都无法最优求解。
不过,对线性情况的理解能为我们进一步理解和实践对抗稳健性提供一些重要的见解,并将帮助我们理解像支持向量机等其它常用的机器学习方法。
二分类
首先考虑二分类的情况:
\[h_\theta(x) = w^T x + b\]其中\(\theta = \{w \in \mathbb{R}^n, b \in \mathbb{R}\}\),类别标签$y \in {+1,-1}$。相应地,定义如下的二分交叉熵(binary cross entropy)损失函数为:
\[\ell(h_\theta(x), y) = \log(1+\exp(-y\cdot h_\theta(x))) \equiv L(y \cdot h_\theta(x))\]将这种形式的损失函数定义$L(z) = \log(1+\exp(-z))$,下文中求解的优化问题都使用这种损失。此处的语义是,分类器对于类别为$+1$预测的概率为:
\[p(y=+1|x) = \frac{1}{1 + \exp(-h_\theta(x))}\]作者再一次贴心地推导了上述损失函数。但这里的符号会引起一些误解,初看的时候晕了好久,我会详细进行说明。
如果使用传统的多分类交叉熵损失,那么对于二分类问题来说,第一种类别的概率是:
\[\frac{\exp(h_\theta(x)_1)}{\exp(h_\theta(x)_1) + \exp(h_\theta(x)_2)} = \frac{1}{1 + \exp(h_\theta(x)_2 - h_\theta(x)_1)}\]类似的,第二种类别的概率为:
\[\frac{\exp(h_\theta(x)_2)}{\exp(h_\theta(x)_1) + \exp(h_\theta(x)_2)} = \frac{1}{1 + \exp(h_\theta(x)_1 - h_\theta(x)_2)}.\]如果我们定义如下的标量假设:
\[h'_\theta(x) \equiv h_\theta(x)_1 - h_\theta(x)_2\]那么对于$y \in {+1,-1}$,相应的概率为:
\[p(y|x) = \frac{1}{1 + \exp(-y\cdot h'_\theta(x))}\]取上述概率的负对数,就是上面定义的binary cross entropy损失函数的形式:
\[-\log \frac{1}{1 + \exp(-y\cdot h'_\theta(x))} = \log(1 + \exp(-y\cdot h'_\theta(x)))\]一开始我很困惑,因为上式中的假设是\(h'_\theta(x)\),而binary cross entropy中使用的却是\(h_\theta(x)\),两者怎么能等价?
其实问题出在我没有从几何的角度去思考线性模型。正如文章中说,用多分类交叉熵损失来考虑二分类问题。在线性模型中,\(h_\theta(x)_i\)是样本空间中将第$i$类与其他类别区分开的一条“分界线”(准确的说应该是超平面),所以上述推导中的\(h_\theta(x)_1\)和\(h_\theta(x)_2\)分别是两条分界线。在二分类情况下,这两条分界线都是将第一类和第二类区别开来,但它们的参数不一定相同,如下图所示:
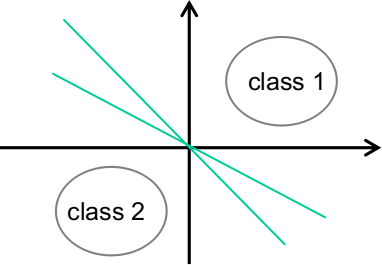
\(h'_\theta(x) \equiv h_\theta(x)_1 - h_\theta(x)_2\)得到的其实是一条新的分界线:
\[h_\theta(x)_1 = w_1^Tx + b_1 \\h_\theta(x)_2 = w_2^Tx + b_2 \\\Rightarrow h'_\theta(x) = h_\theta(x)_1 - h_\theta(x)_2 = ( w_1^T- w_2^T)x + (b_1-b_2)\]这条分界线表示的线性模型将第一类和第二类分开,也就是二分类问题中的线性模型。
求解内部优化问题
接下来考虑稳健优化问题中的内部最大化问题:
\[\DeclareMathOperator*{\maximize}{maximize} \maximize_{\|\delta\| \leq \epsilon} \ell(w^T (x+\delta), y) \equiv \maximize_{\|\delta\| \leq \epsilon} L(y \cdot (w^T(x+\delta) + b)).\]将损失函数画出来可以知道它是一个递减函数:
所以,求解这个函数的最大值只需找到内部标量的最小值即可:
\[% <![CDATA[ \begin{split} \DeclareMathOperator*{\minimize}{minimize} \max_{\|\delta\| \leq \epsilon} L \left(y \cdot (w^T(x+\delta) + b) \right) & = L\left( \min_{\|\delta\| \leq \epsilon} y \cdot (w^T(x+\delta) + b) \right) \\ & = L\left(y\cdot(w^Tx + b) + \min_{\|\delta\| \leq \epsilon} y \cdot w^T\delta \right) \end{split} %]]>\]于是问题转化成为求解如下问题:
\[\min_{\|\delta\| \leq \epsilon} y \cdot w^T\delta.\]为了解决这个问题,我们首先来看$y=+1$和无穷范数\(\|\delta\|_\infty \leq \epsilon\)的情况。为使上式取值最小,只需要在$w_i\geq 0$时令$\delta_i = -\epsilon$,在$w_i< 0$时令$\delta_i = \epsilon$;对于$y=-1$的情况,反之即可。因此,在无穷范数约束下,上述优化问题的解是:
\[\delta^\star = - y \epsilon \cdot \mathrm{sign}(w)\]最小值则为:
\[y \cdot w^T\delta^\star = y \cdot \sum_{i=1} -y \epsilon \cdot \mathrm{sign}(w_i) w_i = -y^2 \epsilon \sum_{i} |w_i| = -\epsilon \|w\|_1.\]相应地,内部最大化问题的值为:
\[\max_{\|\delta\|_\infty \leq \epsilon} L \left(y \cdot (w^T(x+\delta) + b) \right) = L \left(y \cdot (w^Tx + b) - \epsilon \|w\|_1 \right ).\]由于直接求解了内部最大化问题,原来的最大最小优化问题就成了单纯的最小化问题:
\[\minimize_{w,b} \frac{1}{D} \sum_{(x,y) \in D} L \left(y \cdot (w^Tx + b) - \epsilon \|w\|_1 \right ).\]这个问题依然是凸的,故可以准确求解$w$和$b$。
更一般的,上述优化问题的解可以写作:
\[\min_{\|\delta\| \leq \epsilon} y \cdot w^T\delta = -\epsilon \|w\|_*\]其中\(\|\cdot\|_*\)表示的是我们一开始约束在$\theta$上的范数的对偶范数(当$1/p + 1/q = 1$时,\(\|\cdot\|_p\)和\(\|\cdot\|_q\)是对偶范数)。所以不论给扰动施加什么样的范数约束,都可以直接通过对偶范数来求解。
值得注意的是,最后的剩下的这个优化问题
\[\minimize_{w,b} \frac{1}{D} \sum_{(x,y) \in D} L \left(y \cdot (w^Tx + b) - \epsilon \|w\|_1 \right ).\]看起来特别像机器学习中的正则化\(\minimize_{w,b} \frac{1}{D}\sum_{(x,y) \in D} L (y \cdot (w^Tx + b)) + \epsilon \|w\|_*\),只不过这里的正则化项是在损失函数内部。
直观上来看,这意味在稳健性优化问题中,如果一个点远离决策界(decision boundary),即\(w^Tx + b\)的取值较大,由于\(L\)是递减函数,因此不需要惩罚参数的范数;但如果一个点靠近决策界,即\(w^Tx + b\)的取值较小,那么\(L (y \cdot (w^Tx + b))\)的取值则会较大,因此会对参数的范数进行惩罚。这部分内容在SVM中有很多研究。
图示二分类
为了直观地明白线性分类器下的稳健性优化到底发生了什么,作者在MNIST数据集上进行了实验。
首先载入MNIST数据集中0和1两类数据。
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
mnist_train = datasets.MNIST("./data", train=True, download=True, transform=transforms.ToTensor())
mnist_test = datasets.MNIST("./data", train=False, download=True, transform=transforms.ToTensor())
train_idx = mnist_train.train_labels <= 1
mnist_train.train_data = mnist_train.train_data[train_idx]
mnist_train.train_labels = mnist_train.train_labels[train_idx]
test_idx = mnist_test.test_labels <= 1
mnist_test.test_data = mnist_test.test_data[test_idx]
mnist_test.test_labels = mnist_test.test_labels[test_idx]
train_loader = DataLoader(mnist_train, batch_size = 100, shuffle=True)
test_loader = DataLoader(mnist_test, batch_size = 100, shuffle=False)
然后训练一个简单的线性分类器:
import torch
import torch.nn as nn
import torch.optim as optim
# do a single pass over the data
def epoch(loader, model, opt=None):
total_loss, total_err = 0.,0.
for X,y in loader:
yp = model(X.view(X.shape[0], -1))[:,0]
loss = nn.BCEWithLogitsLoss()(yp, y.float())
if opt:
opt.zero_grad()
loss.backward()
opt.step()
total_err += ((yp > 0) * (y==0) + (yp < 0) * (y==1)).sum().item()
total_loss += loss.item() * X.shape[0]
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
model = nn.Linear(784, 1)
opt = optim.SGD(model.parameters(), lr=1.)
print("Train Err", "Train Loss", "Test Err", "Test Loss", sep="\t")
for i in range(10):
train_err, train_loss = epoch(train_loader, model, opt)
test_err, test_loss = epoch(test_loader, model)
print(*("{:.6f}".format(i) for i in (train_err, train_loss, test_err, test_loss)), sep="\t")
Train Err Train Loss Test Err Test Loss
0.007501 0.015405 0.000946 0.003278
0.001342 0.005392 0.000946 0.002892
0.001342 0.004438 0.000473 0.002560
0.001105 0.003788 0.000946 0.002495
0.000947 0.003478 0.000946 0.002297
0.000947 0.003251 0.000946 0.002161
0.000711 0.002940 0.000473 0.002159
0.000790 0.002793 0.000946 0.002109
0.000711 0.002650 0.000946 0.002107
0.000790 0.002529 0.000946 0.001997
训练10轮之后,test loss为0.0004,而且只判断错了一个case。
而我们要施加的扰动,根据上面的推导可以发现,是与$x$无关的:
\[\delta^\star = - y \epsilon \cdot \mathrm{sign}(w),\]即对所有的case都施加该扰动。尽管对于图像而言,施加扰动后的应该使得$x+\delta$在$[0,1]$区间内,不过对于模型来说,超过区间的数值并不会影响计算。所以在本例中作者没有刻意去处理这一点,只会在展示的时候做相应地值进行裁剪(clip values)。
将所施加的扰动画出来:
epsilon = 0.2
delta = epsilon * model.weight.detach().sign().view(28,28)
plt.imshow(1-delta.numpy(), cmap="gray")
接着来看将该对抗攻击施加到测试集上的效果:
def epoch_adv(loader, model, delta):
total_loss, total_err = 0.,0.
for X,y in loader:
yp = model((X-(2*y.float()[:,None,None,None]-1)*delta).view(X.shape[0], -1))[:,0]
loss = nn.BCEWithLogitsLoss()(yp, y.float())
total_err += ((yp > 0) * (y==0) + (yp < 0) * (y==1)).sum().item()
total_loss += loss.item() * X.shape[0]
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
print(epoch_adv(test_loader, model, delta[None,None,:,:]))
(0.8458628841607565, 3.4517438034075654)
代码中的$2*y.float()-1$是将原本的$0/1$映射成$-1/+1$
可以看到,在$\epsilon=0.2$的$\ell_\infty$球扰动下,分类器在测试集上的误差从几乎为零变成了$84.5\%$。和Chapter 1中ImageNet的例子不同,这里施加扰动后的图像可以清楚看出不同(只是将上面图示的扰动叠加到图像上),但这种程度的扰动完全不足以欺骗大多数人类。
f,ax = plt.subplots(5,5, sharey=True)
for i in range(25):
ax[i%5][i//5].imshow(1-(X_test[i].view(28,28) - (2*y_test[i]-1)*delta).numpy(), cmap="gray")
ax
训练稳健的线性模型
见识了对抗攻击对正常训练的线性模型的影响,我们再对线性模型做稳健性优化。前面的推导告诉我们可以直接将$\ell_1$范数添加到目标函数上(求解最小最大优化问题)。具体的,从输入$x$减去\(\epsilon(2y-1)\|w\|_1\)。
# do a single pass over the data
def epoch_robust(loader, model, epsilon, opt=None):
total_loss, total_err = 0.,0.
for X,y in loader:
yp = model(X.view(X.shape[0], -1))[:,0] - epsilon*(2*y.float()-1)*model.weight.norm(1)
loss = nn.BCEWithLogitsLoss()(yp, y.float())
if opt:
opt.zero_grad()
loss.backward()
opt.step()
total_err += ((yp > 0) * (y==0) + (yp < 0) * (y==1)).sum().item()
total_loss += loss.item() * X.shape[0]
return total_err / len(loader.dataset), total_loss / len(loader.dataset)
model = nn.Linear(784, 1)
opt = optim.SGD(model.parameters(), lr=1e-1)
epsilon = 0.2
print("Rob. Train Err", "Rob. Train Loss", "Rob. Test Err", "Rob. Test Loss", sep="\t")
for i in range(20):
train_err, train_loss = epoch_robust(train_loader, model, epsilon, opt)
test_err, test_loss = epoch_robust(test_loader, model, epsilon)
print(*("{:.6f}".format(i) for i in (train_err, train_loss, test_err, test_loss)), sep="\t")
Rob. Train Err Rob. Train Loss Rob. Test Err Rob. Test Loss
0.147414 0.376791 0.073759 0.228654
0.073352 0.223381 0.053901 0.176481
0.062929 0.197301 0.043026 0.154818
0.057008 0.183879 0.038298 0.139773
0.052981 0.174964 0.040662 0.143639
0.050059 0.167973 0.037352 0.132365
0.048164 0.162836 0.032624 0.119755
0.046190 0.158340 0.033570 0.123211
0.044769 0.154719 0.029787 0.118066
0.043979 0.152048 0.027423 0.118974
0.041058 0.149381 0.026478 0.110074
0.040268 0.147034 0.027423 0.114998
0.039874 0.145070 0.026950 0.109395
0.038452 0.143232 0.026950 0.109015
0.037663 0.141919 0.027896 0.113093
0.036715 0.140546 0.026478 0.103066
0.036321 0.139162 0.026478 0.107028
0.035610 0.138088 0.025059 0.104717
0.035215 0.137290 0.025059 0.104803
0.034741 0.136175 0.025059 0.106629
通过对抗性训练,原本线性模型在对抗攻击下的错误率高达$85\%$,如今降低到了只有$2.5\%$。但我们很好奇,这样的一个模型在非对抗攻击的数据集上会有什么表现?
train_err, train_loss = epoch(train_loader, model)
test_err, test_loss = epoch(test_loader, model)
print("Train Err", "Train Loss", "Test Err", "Test Loss", sep="\t")
print(*("{:.6f}".format(i) for i in (train_err, train_loss, test_err, test_loss)), sep="\t")
Train Err Train Loss Test Err Test Loss
0.006080 0.015129 0.003783 0.008186
可以看到,在测试集上的误差是$0.3\%$,表现并不如标准训练模式下的模型。原本只预测错了1个case,现在却预测错了8个case。这并不是巧合,相反,在标准的准确率和稳健性准确率之间可能存在着某种基本的折衷:如果想要降低稳健性误差,就会导致标准误差升高。之后会再来讨论这一问题。
最后我们来看看对这个稳健性模型而言的最优扰动是什么样的。
delta = epsilon * model.weight.detach().sign().view(28,28)
plt.imshow(1-delta.numpy(), cmap="gray")
看上去非常像数字0。于是,我们可以得到一些证据(诚然,这样的证据还很weak)来证明稳健性训练或许是在让“对抗性的方向”上更有意义。我们并不是通过添加“随机噪声”来欺骗分类器,实际上是在将一幅图像朝着另一幅新图像的方向上移动。
</br>